Tissot's indicatrix

Tissot's indicatrix is a way to characterize local distortions in a map projection (see the Wikipedia article).

It is traditionally constructed by differentiating the projection. However, we can implement a similar indicatrix in a more straightforward way, by simply projecting circles formed on the ellipsoidal Earth onto a map.

Here' we'll show how you can do this for a few projections.

using Proj, GeoMakie, CairoMakie
import GeometryBasics: Point2d
import GeometryOps as GO

First, we define a function that gets a geodesic circle around some given point:

function geodesic_circle(origin::PointType, radius::Real, npoints = 100; geodesic = Proj.geod_geodesic(6378137, 1/298.257223563)) where PointType <: Point2
    points = [PointType(Proj.geod_direct(geodesic, origin[2], origin[1], θ, radius)[[2, 1]]) for θ in LinRange(0, 360, npoints)]
    if points[end] != points[begin]
        points[end] = points[begin]
    end
    return points
end
poly(geodesic_circle(Point2f(0, 65), 100_000); axis = (; aspect = DataAspect()))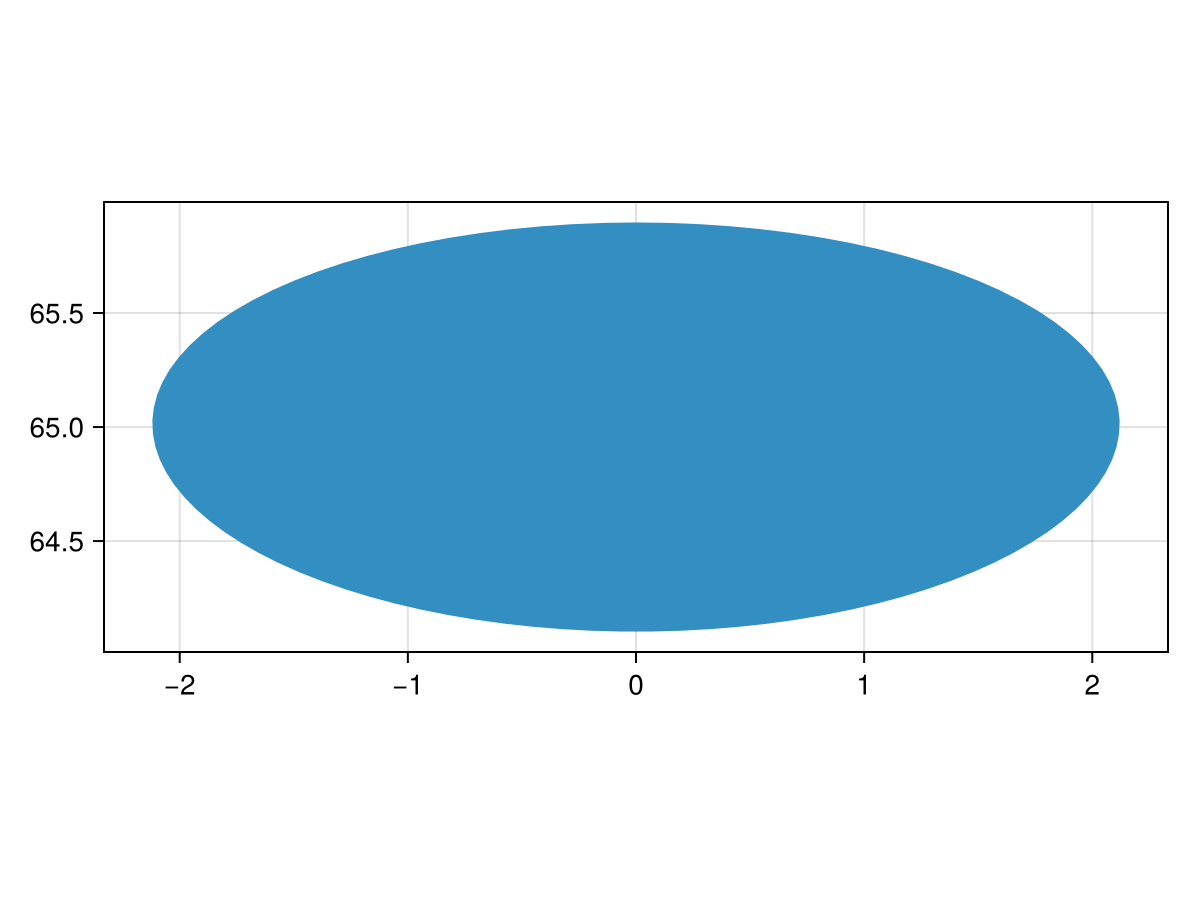

Note the curvature of the polygon - this is because it's the locus of points which are radius away from origin on the ellipsoidal Earth, not the flat Earth!

Now, we can create a proper Tissot map. Let's examine the Bertin 1953 projection.

f, a, p = lines(GeoMakie.coastlines(); axis = (; type = GeoAxis, dest = "+proj=bertin1953"))
f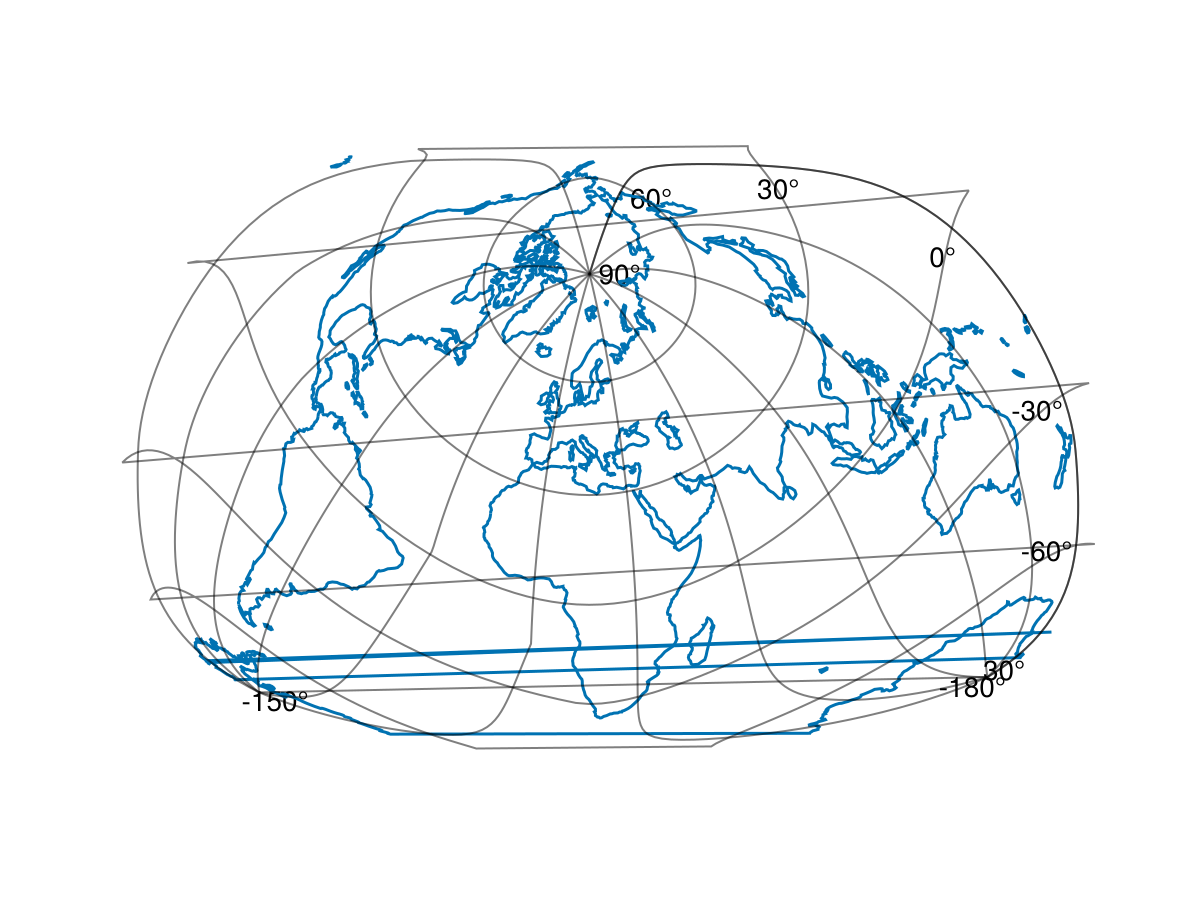

Now, we cn add the Tissot polygons:

lons = LinRange(-180, 180, 13)
lats = LinRange(-90, 90, 7)
circle_polys = [GO.GI.Polygon([geodesic_circle(Point2d(lon, lat), 500_000, 50)]) for lon in lons, lat in lats] |> vec

91-element Vector{GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{GeometryBasics.Point{2, Float64}}, Nothing, Nothing}}, Nothing, Nothing}}:
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-180.0, -85.52339101263448], … (48) … , [-180.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-150.0, -85.52339101263448], … (48) … , [-150.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-120.0, -85.52339101263448], … (48) … , [-120.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-90.0, -85.52339101263448], … (48) … , [-90.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-60.000000000000014, -85.52339101263448], … (48) … , [-60.000000000000014, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-29.999999999999986, -85.52339101263448], … (48) … , [-29.999999999999986, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[0.0, -85.52339101263448], … (48) … , [0.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[30.0, -85.52339101263448], … (48) … , [30.0, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[59.99999999999999, -85.52339101263448], … (48) … , [59.99999999999999, -85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[90.0, -85.52339101263448], … (48) … , [90.0, -85.52339101263448]])])
 ⋮
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[119.99999999999999, 85.52339101263448], … (48) … , [119.99999999999999, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[150.0, 85.52339101263448], … (48) … , [150.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[180.0, 85.52339101263448], … (48) … , [180.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-150.0, 85.52339101263448], … (48) … , [-150.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-120.0, 85.52339101263448], … (48) … , [-120.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-90.0, 85.52339101263448], … (48) … , [-90.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-60.0, 85.52339101263448], … (48) … , [-60.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[-30.0, 85.52339101263448], … (48) … , [-30.0, 85.52339101263448]])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[0.0, 85.52339101263448], … (48) … , [0.0, 85.52339101263448]])])

circle_polys_cut = GO.cut.(circle_polys, (GO.GI.Line(Point2d[(0, -180), (0, 180)]),)) .|> GO.GI.MultiPolygon # hide

poly!(a, circle_polys; color = Makie.wong_colors(0.7)[2])
f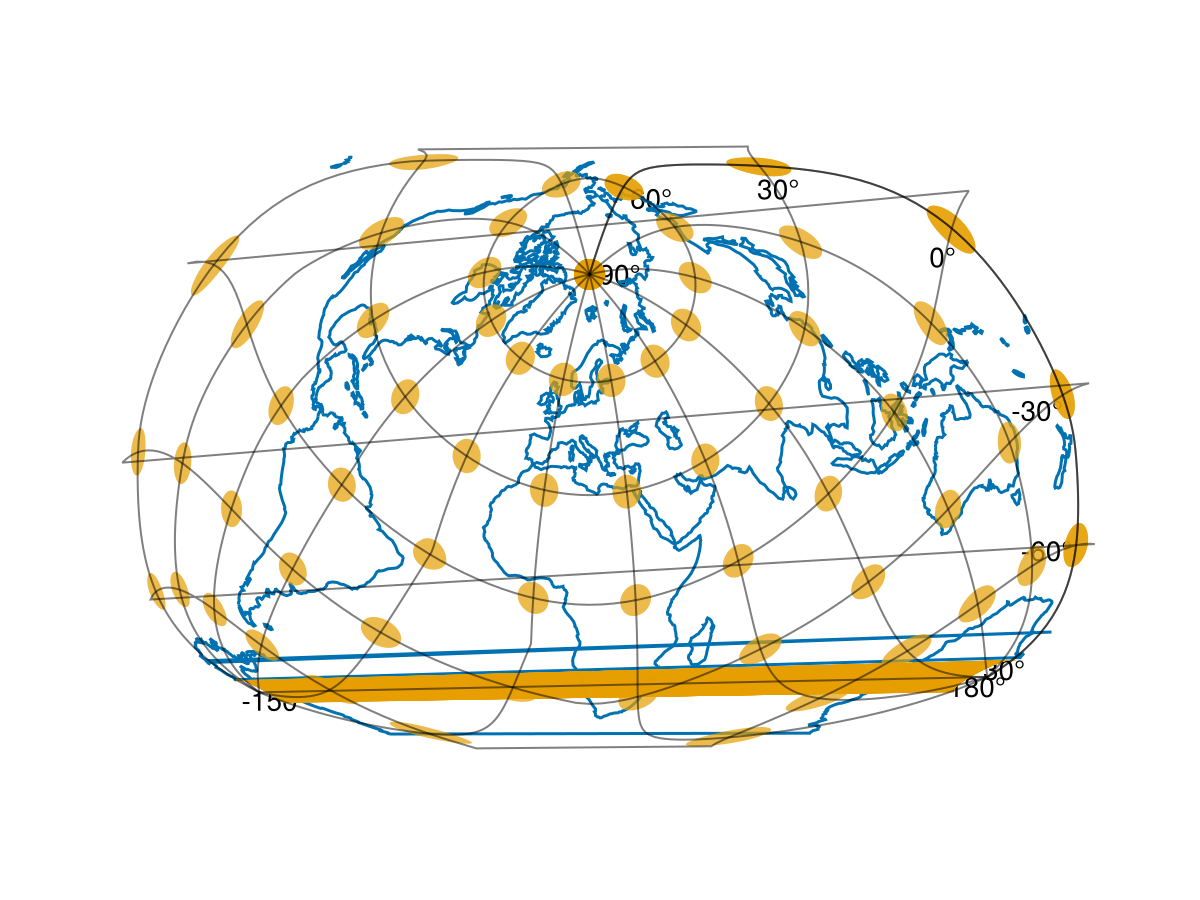

---

This page was generated using Literate.jl.