Graphs on maps
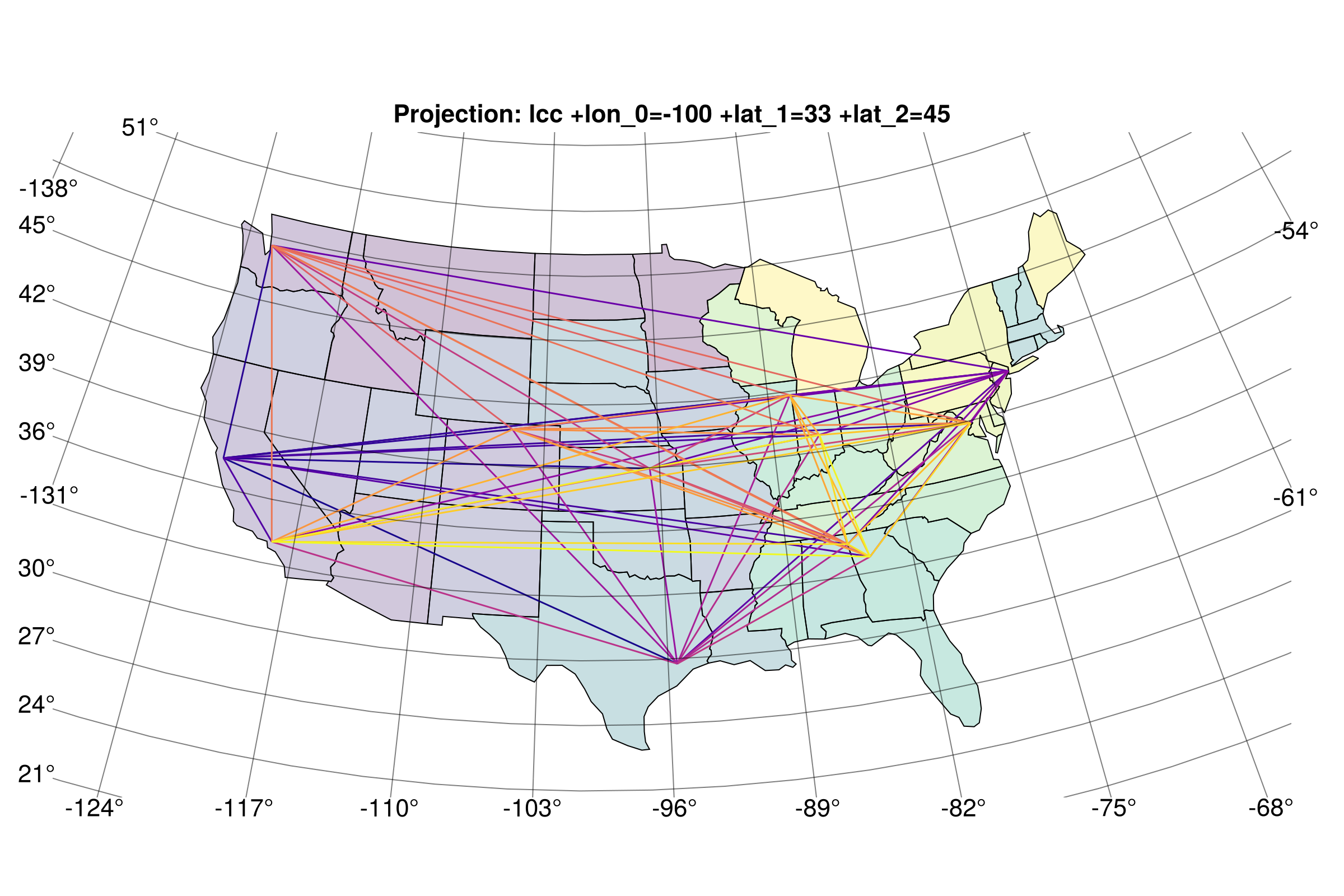
Any Makie recipe can be plotted onto a GeoAxis``, and this includes recipes like GraphMakie'sgraphplot`, complex though it may be!
In this example, we'll show how to plot a graph onto a choropleth map (it's really as simple as plotting it onto a normal Axis, just using a GeoAxis instead).
This example was adapted from code in this Julia Discourse post.
using GeoMakie, CairoMakie
using GraphMakie, GraphMakie.Graphs
using NaturalEarth, DataFramesWe get US state borders from Natural Earth, and filter it out so it's only the continental states. For the purposes of this example, we only care about those.
admin_1_df = DataFrame(naturalearth("admin_1_states_provinces", 110))| Row | FCLASS_IL | FCLASS_US | FCLASS_AR | wikipedia | name_en | FCLASS_FR | admin | gns_lang | gu_a3 | name_tr | name_ko | name | geonunit | gn_a1_code | name_nl | FCLASS_JP | name_fr | FCLASS_SE | name_alt | type_en | wikidataid | adm0_sr | name_pt | FCLASS_TLC | gns_id | sub_code | longitude | mapcolor13 | gns_region | region | gn_name | gns_level | region_sub | scalerank | name_ar | max_label | name_zht | name_fa | FCLASS_PL | postal | latitude | check_me | name_sv | FCLASS_IN | FCLASS_BR | FCLASS_UA | name_hu | sameascity | code_hasc | code_local | woe_id | FCLASS_BD | FCLASS_GB | labelrank | sov_a3 | FCLASS_PT | FCLASS_KO | FCLASS_NP | featurecla | min_zoom | gns_adm1 | adm1_code | name_bn | name_he | name_de | fips | name_el | woe_name | FCLASS_MA | name_len | fips_alt | FCLASS_PS | name_ja | datarank | FCLASS_ISO | diss_me | region_cod | gns_name | mapcolor9 | adm0_label | FCLASS_TR | FCLASS_SA | name_zh | area_sqkm | iso_3166_2 | name_local | abbrev | name_vi | name_it | FCLASS_DE | woe_label | FCLASS_VN | name_ur | FCLASS_IT | geometry | min_label | gn_region | note | name_pl | FCLASS_ES | iso_a2 | hasc_maybe | name_es | FCLASS_CN | provnum_ne | name_id | FCLASS_TW | name_ru | FCLASS_EG | FCLASS_GR | adm0_a3 | FCLASS_ID | FCLASS_NL | FCLASS_PK | name_uk | gadm_level | type | gn_id | gn_level | ne_id | name_hi | FCLASS_RU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Missing | Missing | Missing | String | String | Missing | String | Missing | String | String | String | String | String | String | String | Missing | String | Missing | String | String | String | Int64 | String | Missing | Int64 | Missing | Float64 | Int64 | Missing | String | String | Int64 | String | Int64 | String | Float64 | String | String | Missing | String | Float64 | Int64 | String | Missing | Missing | Missing | String | Int64 | String | String | Int64 | Missing | Missing | Int64 | String | Missing | Missing | Missing | String | Int64 | Missing | String | String | String | String | String | String | String | Missing | Int64 | String? | Missing | String | Int64 | Missing | Int64 | Missing | Missing | Int64 | Int64 | Missing | Missing | String | Int64 | String | Missing | String | String | String | Missing | String | Missing | String | Missing | Union… | Float64 | Missing | Missing | String | Missing | String | String? | String | Missing | Int64 | String | Missing | String | Missing | Missing | String | Missing | Missing | Missing | String | Int64 | String | Int64 | Int64 | Int64 | String | Missing | |
| 1 | missing | missing | missing | http://en.wikipedia.org/wiki/Minnesota | Minnesota | missing | United States of America | missing | USA | Minnesota | 미네소타 | Minnesota | United States of America | US.MN | Minnesota | missing | Minnesota | missing | MN|Minn. | State | Q1527 | 1 | Minnesota | missing | -1 | missing | -93.364 | 1 | missing | Midwest | Minnesota | -1 | West North Central | 2 | مينيسوتا | 7.5 | 明尼蘇達州 | مینهسوتا | missing | MN | 46.0592 | 20 | Minnesota | missing | missing | missing | Minnesota | -99 | US.MN | US27 | 2347582 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3514 | মিনেসোটা | מינסוטה | Minnesota | US27 | Μινεσότα | Minnesota | missing | 9 | missing | missing | ミネソタ州 | 1 | missing | 3514 | missing | missing | 1 | 2 | missing | missing | 明尼苏达州 | 0 | US-MN | missing | Minn. | Minnesota | Minnesota | missing | Minnesota, US, United States | missing | مینیسوٹا | missing | 2D Polygon | 3.5 | missing | missing | Minnesota | missing | US | missing | Minnesota | missing | 0 | Minnesota | missing | Миннесота | missing | missing | USA | missing | missing | missing | Міннесота | 1 | State | 5037779 | 1 | 1159315297 | मिनेसोटा | missing |
| 2 | missing | missing | missing | http://en.wikipedia.org/wiki/Montana | Montana | missing | United States of America | missing | USA | Montana | 몬태나 | Montana | United States of America | US.MT | Montana | missing | Montana | missing | MT|Mont. | State | Q1212 | 1 | Montana | missing | -1 | missing | -110.044 | 1 | missing | West | Montana | -1 | Mountain | 2 | مونتانا | 7.5 | 蒙大拿州 | ایالت مونتانا | missing | MT | 46.9965 | 20 | Montana | missing | missing | missing | Montana | -99 | US.MT | US30 | 2347585 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3515 | মন্টানা | מונטנה | Montana | US30 | Μοντάνα | Montana | missing | 7 | missing | missing | モンタナ州 | 1 | missing | 3515 | missing | missing | 1 | 2 | missing | missing | 蒙大拿州 | 0 | US-MT | missing | Mont. | Montana | Montana | missing | Montana, US, United States | missing | مونٹانا | missing | 2D Polygon | 3.5 | missing | missing | Montana | missing | US | missing | Montana | missing | 0 | Montana | missing | Монтана | missing | missing | USA | missing | missing | missing | Монтана | 1 | State | 5667009 | 1 | 1159315333 | मोन्टाना | missing |
| 3 | missing | missing | missing | http://en.wikipedia.org/wiki/North_Dakota | North Dakota | missing | United States of America | missing | USA | Kuzey Dakota | 노스다코타 | North Dakota | United States of America | US.ND | Noord-Dakota | missing | Dakota du Nord | missing | ND|N.D. | State | Q1207 | 1 | Dakota do Norte | missing | -1 | missing | -100.302 | 1 | missing | Midwest | North Dakota | -1 | West North Central | 2 | داكوتا الشمالية | 7.5 | 北達科他州 | داکوتای شمالی | missing | ND | 47.4675 | 20 | North Dakota | missing | missing | missing | Észak-Dakota | -99 | US.ND | US38 | 2347593 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3516 | নর্থ ডাকোটা | דקוטה הצפונית | North Dakota | US38 | Βόρεια Ντακότα | North Dakota | missing | 12 | missing | missing | ノースダコタ州 | 1 | missing | 3516 | missing | missing | 1 | 2 | missing | missing | 北达科他州 | 0 | US-ND | missing | N.D. | Bắc Dakota | Dakota del Nord | missing | North Dakota, US, United States | missing | شمالی ڈکوٹا | missing | 2D Polygon | 3.5 | missing | missing | Dakota Północna | missing | US | missing | Dakota del Norte | missing | 0 | Dakota Utara | missing | Северная Дакота | missing | missing | USA | missing | missing | missing | Північна Дакота | 1 | State | 5690763 | 1 | 1159315337 | उत्तर डेकोटा | missing |
| 4 | missing | missing | missing | http://en.wikipedia.org/wiki/Hawaii | Hawaii | missing | United States of America | missing | USA | Hawaii | 하와이 | Hawaii | United States of America | US.HI | Hawaï | missing | Hawaï | missing | HI|Hawaii | State | Q782 | 8 | Havaí | missing | -1 | missing | -157.999 | 1 | missing | West | Hawaii | -1 | Pacific | 2 | هاواي | 7.5 | 夏威夷州 | هاوائی | missing | HI | 21.4919 | 20 | Hawaii | missing | missing | missing | Hawaii | -99 | US.HI | US15 | 2347570 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3517 | হাওয়াই | הוואי | Hawaii | US15 | Χαβάη | Hawaii | missing | 6 | missing | missing | ハワイ州 | 1 | missing | 3517 | missing | missing | 1 | 2 | missing | missing | 夏威夷州 | 0 | US-HI | missing | Hawaii | Hawaii | Hawaii | missing | Hawaii, US, United States | missing | ہوائی | missing | 2D MultiPolygon | 3.5 | missing | missing | Hawaje | missing | US | missing | Hawái | missing | 0 | Hawaii | missing | Гавайи | missing | missing | USA | missing | missing | missing | Гаваї | 1 | State | 5855797 | 1 | 1159308409 | हवाई | missing |
| 5 | missing | missing | missing | http://en.wikipedia.org/wiki/Idaho | Idaho | missing | United States of America | missing | USA | Idaho | 아이다호 | Idaho | United States of America | US.ID | Idaho | missing | Idaho | missing | ID|Idaho | State | Q1221 | 1 | Idaho | missing | -1 | missing | -114.133 | 1 | missing | West | Idaho | -1 | Mountain | 2 | أيداهو | 7.5 | 愛達荷州 | آیداهو | missing | ID | 43.7825 | 20 | Idaho | missing | missing | missing | Idaho | -99 | US.ID | US16 | 2347571 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3518 | আইডাহো | איידהו | Idaho | US16 | Άινταχο | Idaho | missing | 5 | missing | missing | アイダホ州 | 1 | missing | 3518 | missing | missing | 1 | 2 | missing | missing | 爱达荷州 | 0 | US-ID | missing | Idaho | Idaho | Idaho | missing | Idaho, US, United States | missing | ایڈاہو | missing | 2D Polygon | 3.5 | missing | missing | Idaho | missing | US | missing | Idaho | missing | 0 | Idaho | missing | Айдахо | missing | missing | USA | missing | missing | missing | Айдахо | 1 | State | 5596512 | 1 | 1159315339 | आयडाहो | missing |
| 6 | missing | missing | missing | http://en.wikipedia.org/wiki/Washington_(state) | Washington | missing | United States of America | missing | USA | Vaşington | 워싱턴 | Washington | United States of America | US.WA | Washington | missing | Washington | missing | WA|Wash. | State | Q1223 | 6 | Washington | missing | -1 | missing | -120.361 | 1 | missing | West | Washington | -1 | Pacific | 2 | واشنطن | 7.5 | 華盛頓州 | ایالت واشینگتن | missing | WA | 47.4865 | 20 | Washington | missing | missing | missing | Washington | -99 | US.WA | US53 | 2347606 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3519 | ওয়াশিংটন | וושינגטון | Washington | US53 | Ουάσινγκτον | Washington | missing | 10 | missing | missing | ワシントン州 | 1 | missing | 3519 | missing | missing | 1 | 2 | missing | missing | 华盛顿州 | 0 | US-WA | missing | Wash. | Washington | Washington | missing | Washington, US, United States | missing | ریاست واشنگٹن | missing | 2D Polygon | 3.5 | missing | missing | Waszyngton | missing | US | missing | Washington | missing | 0 | Washington | missing | Вашингтон | missing | missing | USA | missing | missing | missing | Вашингтон | 1 | State | 5815135 | 1 | 1159309547 | वॉशिंगटन राज्य | missing |
| 7 | missing | missing | missing | http://en.wikipedia.org/wiki/Arizona | Arizona | missing | United States of America | missing | USA | Arizona | 애리조나 | Arizona | United States of America | US.AZ | Arizona | missing | Arizona | missing | AZ|Ariz. | State | Q816 | 1 | Arizona | missing | -1 | missing | -111.935 | 1 | missing | West | Arizona | -1 | Mountain | 2 | أريزونا | 7.5 | 亞利桑那州 | آریزونا | missing | AZ | 34.3046 | 20 | Arizona | missing | missing | missing | Arizona | -99 | US.AZ | US04 | 2347561 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3520 | অ্যারিজোনা | אריזונה | Arizona | US04 | Αριζόνα | Arizona | missing | 7 | missing | missing | アリゾナ州 | 1 | missing | 3520 | missing | missing | 1 | 2 | missing | missing | 亚利桑那州 | 0 | US-AZ | missing | Ariz. | Arizona | Arizona | missing | Arizona, US, United States | missing | ایریزونا | missing | 2D Polygon | 3.5 | missing | missing | Arizona | missing | US | missing | Arizona | missing | 0 | Arizona | missing | Аризона | missing | missing | USA | missing | missing | missing | Аризона | 1 | State | 5551752 | 1 | 1159315341 | एरीजोना | missing |
| 8 | missing | missing | missing | http://en.wikipedia.org/wiki/California | California | missing | United States of America | missing | USA | Kaliforniya | 캘리포니아 | California | United States of America | US.CA | Californië | missing | Californie | missing | CA|Calif. | State | Q99 | 8 | Califórnia | missing | -1 | missing | -119.591 | 1 | missing | West | California | -1 | Pacific | 2 | كاليفورنيا | 7.5 | 加利福尼亞州 | کالیفرنیا | missing | CA | 36.7496 | 20 | Kalifornien | missing | missing | missing | Kalifornia | -99 | US.CA | US06 | 2347563 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3521 | ক্যালিফোর্নিয়া | קליפורניה | Kalifornien | US06 | Καλιφόρνια | California | missing | 10 | missing | missing | カリフォルニア州 | 1 | missing | 3521 | missing | missing | 1 | 2 | missing | missing | 加利福尼亚州 | 0 | US-CA | missing | Calif. | California | California | missing | California, US, United States | missing | کیلی فورنیا | missing | 2D Polygon | 3.5 | missing | missing | Kalifornia | missing | US | missing | California | missing | 0 | California | missing | Калифорния | missing | missing | USA | missing | missing | missing | Каліфорнія | 1 | State | 5332921 | 1 | 1159308415 | कैलिफ़ोर्निया | missing |
| 9 | missing | missing | missing | http://en.wikipedia.org/wiki/Colorado | Colorado | missing | United States of America | missing | USA | Colorado | 콜로라도 | Colorado | United States of America | US.CO | Colorado | missing | Colorado | missing | CO|Colo. | State | Q1261 | 1 | Colorado | missing | -1 | missing | -105.543 | 1 | missing | West | Colorado | -1 | Mountain | 2 | كولورادو | 7.5 | 科羅拉多州 | کلرادو | missing | CO | 38.9998 | 20 | Colorado | missing | missing | missing | Colorado | -99 | US.CO | US08 | 2347564 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3522 | কলোরাডো | קולורדו | Colorado | US08 | Κολοράντο | Colorado | missing | 8 | missing | missing | コロラド州 | 1 | missing | 3522 | missing | missing | 1 | 2 | missing | missing | 科罗拉多州 | 0 | US-CO | missing | Colo. | Colorado | Colorado | missing | Colorado, US, United States | missing | کولوراڈو | missing | 2D Polygon | 3.5 | missing | missing | Kolorado | missing | US | missing | Colorado | missing | 0 | Colorado | missing | Колорадо | missing | missing | USA | missing | missing | missing | Колорадо | 1 | State | 5417618 | 1 | 1159315343 | कॉलराडो | missing |
| 10 | missing | missing | missing | http://en.wikipedia.org/wiki/Nevada | Nevada | missing | United States of America | missing | USA | Nevada | 네바다 | Nevada | United States of America | US.NV | Nevada | missing | Nevada | missing | NV|Nev. | State | Q1227 | 1 | Nevada | missing | -1 | missing | -117.02 | 1 | missing | West | Nevada | -1 | Mountain | 2 | نيفادا | 7.5 | 內華達州 | نوادا | missing | NV | 39.4299 | 20 | Nevada | missing | missing | missing | Nevada | -99 | US.NV | US32 | 2347587 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3523 | নেভাডা | נבדה | Nevada | US32 | Νεβάδα | Nevada | missing | 6 | missing | missing | ネバダ州 | 1 | missing | 3523 | missing | missing | 1 | 2 | missing | missing | 内华达州 | 0 | US-NV | missing | Nev. | Nevada | Nevada | missing | Nevada, US, United States | missing | نیواڈا | missing | 2D Polygon | 3.5 | missing | missing | Nevada | missing | US | missing | Nevada | missing | 0 | Nevada | missing | Невада | missing | missing | USA | missing | missing | missing | Невада | 1 | State | 5509151 | 1 | 1159315345 | नेवाडा | missing |
| 11 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Mexico | New Mexico | missing | United States of America | missing | USA | New Mexico | 뉴멕시코 | New Mexico | United States of America | US.NM | New Mexico | missing | Nouveau-Mexique | missing | NM|N.M. | State | Q1522 | 1 | Novo México | missing | -1 | missing | -106.024 | 1 | missing | West | New Mexico | -1 | Mountain | 2 | نيومكسيكو | 7.5 | 新墨西哥州 | نیومکزیکو | missing | NM | 34.5002 | 20 | New Mexico | missing | missing | missing | Új-Mexikó | -99 | US.NM | US35 | 2347590 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3524 | নিউ মেক্সিকো | ניו מקסיקו | New Mexico | US35 | Νέο Μεξικό | New Mexico | missing | 10 | missing | missing | ニューメキシコ州 | 1 | missing | 3524 | missing | missing | 1 | 2 | missing | missing | 新墨西哥州 | 0 | US-NM | missing | N.M. | New Mexico | Nuovo Messico | missing | New Mexico, US, United States | missing | نیو میکسیکو | missing | 2D Polygon | 3.5 | missing | missing | Nowy Meksyk | missing | US | missing | Nuevo México | missing | 0 | New Mexico | missing | Нью-Мексико | missing | missing | USA | missing | missing | missing | Нью-Мексико | 1 | State | 5481136 | 1 | 1159315347 | नया मेक्सिको | missing |
| 12 | missing | missing | missing | http://en.wikipedia.org/wiki/Oregon | Oregon | missing | United States of America | missing | USA | Oregon | 오리건 | Oregon | United States of America | US.OR | Oregon | missing | Oregon | missing | OR|Ore. | State | Q824 | 6 | Oregon | missing | -1 | missing | -120.386 | 1 | missing | West | Oregon | -1 | Pacific | 2 | أوريغون | 7.5 | 奧勒岡州 | اورگن | missing | OR | 43.8333 | 20 | Oregon | missing | missing | missing | Oregon | -99 | US.OR | US41 | 2347596 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3525 | অরেগন | אורגון | Oregon | US41 | Όρεγκον | Oregon | missing | 6 | missing | missing | オレゴン州 | 1 | missing | 3525 | missing | missing | 1 | 2 | missing | missing | 俄勒冈州 | 0 | US-OR | missing | Ore. | Oregon | Oregon | missing | Oregon, US, United States | missing | اوریگون | missing | 2D Polygon | 3.5 | missing | missing | Oregon | missing | US | missing | Oregón | missing | 0 | Oregon | missing | Орегон | missing | missing | USA | missing | missing | missing | Орегон | 1 | State | 5744337 | 1 | 1159309549 | औरिगन | missing |
| 13 | missing | missing | missing | http://en.wikipedia.org/wiki/Utah | Utah | missing | United States of America | missing | USA | Utah | 유타 | Utah | United States of America | US.UT | Utah | missing | Utah | missing | UT | State | Q829 | 1 | Utah | missing | -1 | missing | -111.544 | 1 | missing | West | Utah | -1 | Mountain | 2 | يوتا | 7.5 | 猶他州 | یوتا | missing | UT | 39.5007 | 20 | Utah | missing | missing | missing | Utah | -99 | US.UT | US49 | 2347603 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3526 | ইউটা | יוטה | Utah | US49 | Γιούτα | Utah | missing | 4 | missing | missing | ユタ州 | 1 | missing | 3526 | missing | missing | 1 | 2 | missing | missing | 犹他州 | 0 | US-UT | missing | Utah | Utah | Utah | missing | Utah, US, United States | missing | یوٹاہ | missing | 2D Polygon | 3.5 | missing | missing | Utah | missing | US | missing | Utah | missing | 0 | Utah | missing | Юта | missing | missing | USA | missing | missing | missing | Юта | 1 | State | 5549030 | 1 | 1159315349 | यूटाह | missing |
| 14 | missing | missing | missing | http://en.wikipedia.org/wiki/Wyoming | Wyoming | missing | United States of America | missing | USA | Wyoming | 와이오밍 | Wyoming | United States of America | US.WY | Wyoming | missing | Wyoming | missing | WY|Wyo. | State | Q1214 | 1 | Wyoming | missing | -1 | missing | -107.552 | 1 | missing | West | Wyoming | -1 | Mountain | 2 | وايومنغ | 7.5 | 懷俄明州 | وایومینگ | missing | WY | 42.9999 | 20 | Wyoming | missing | missing | missing | Wyoming | -99 | US.WY | US56 | 2347609 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3527 | ওয়াইয়োমিং | ויומינג | Wyoming | US56 | Ουαϊόμινγκ | Wyoming | missing | 7 | missing | missing | ワイオミング州 | 1 | missing | 3527 | missing | missing | 1 | 2 | missing | missing | 怀俄明州 | 0 | US-WY | missing | Wyo. | Wyoming | Wyoming | missing | Wyoming, US, United States | missing | وائیومنگ | missing | 2D Polygon | 3.5 | missing | missing | Wyoming | missing | US | missing | Wyoming | missing | 0 | Wyoming | missing | Вайоминг | missing | missing | USA | missing | missing | missing | Вайомінг | 1 | State | 5843591 | 1 | 1159315351 | वायोमिंग | missing |
| 15 | missing | missing | missing | http://en.wikipedia.org/wiki/Arkansas | Arkansas | missing | United States of America | missing | USA | Arkansas | 아칸소 | Arkansas | United States of America | US.AR | Arkansas | missing | Arkansas | missing | AR|Ark. | State | Q1612 | 1 | Arkansas | missing | -1 | missing | -92.1428 | 1 | missing | South | Arkansas | -1 | West South Central | 2 | أركنساس | 7.5 | 阿肯色州 | آرکانزاس | missing | AR | 34.7563 | 20 | Arkansas | missing | missing | missing | Arkansas | -99 | US.AR | US05 | 2347562 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3528 | আর্কানসাস | ארקנסו | Arkansas | US05 | Άρκανσο | Arkansas | missing | 8 | missing | missing | アーカンソー州 | 1 | missing | 3528 | missing | missing | 1 | 2 | missing | missing | 阿肯色州 | 0 | US-AR | missing | Ark. | Arkansas | Arkansas | missing | Arkansas, US, United States | missing | آرکنساس | missing | 2D Polygon | 3.5 | missing | missing | Arkansas | missing | US | missing | Arkansas | missing | 0 | Arkansas | missing | Арканзас | missing | missing | USA | missing | missing | missing | Арканзас | 1 | State | 4099753 | 1 | 1159315355 | अरकांसास | missing |
| 16 | missing | missing | missing | http://en.wikipedia.org/wiki/Iowa | Iowa | missing | United States of America | missing | USA | Iowa | 아이오와 | Iowa | United States of America | US.IA | Iowa | missing | Iowa | missing | IA|Iowa | State | Q1546 | 1 | Iowa | missing | -1 | missing | -93.3891 | 1 | missing | Midwest | Iowa | -1 | West North Central | 2 | آيوا | 7.5 | 愛荷華州 | آیووا | missing | IA | 42.0423 | 20 | Iowa | missing | missing | missing | Iowa | -99 | US.IA | US19 | 2347574 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3529 | আইওয়া | איווה | Iowa | US19 | Άιοβα | Iowa | missing | 4 | missing | missing | アイオワ州 | 1 | missing | 3529 | missing | missing | 1 | 2 | missing | missing | 艾奥瓦州 | 0 | US-IA | missing | Iowa | Iowa | Iowa | missing | Iowa, US, United States | missing | آئیووا | missing | 2D Polygon | 3.5 | missing | missing | Iowa | missing | US | missing | Iowa | missing | 0 | Iowa | missing | Айова | missing | missing | USA | missing | missing | missing | Айова | 1 | State | 4862182 | 1 | 1159315357 | आयोवा | missing |
| 17 | missing | missing | missing | http://en.wikipedia.org/wiki/Kansas | Kansas | missing | United States of America | missing | USA | Kansas | 캔자스 | Kansas | United States of America | US.KS | Kansas | missing | Kansas | missing | KS|Kans. | State | Q1558 | 1 | Kansas | missing | -1 | missing | -98.3309 | 1 | missing | Midwest | Kansas | -1 | West North Central | 2 | كانساس | 7.5 | 堪薩斯州 | کانزاس | missing | KS | 38.5 | 20 | Kansas | missing | missing | missing | Kansas | -99 | US.KS | US20 | 2347575 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3530 | ক্যান্সাস | קנזס | Kansas | US20 | Κάνσας | Kansas | missing | 6 | missing | missing | カンザス州 | 1 | missing | 3530 | missing | missing | 1 | 2 | missing | missing | 堪萨斯州 | 0 | US-KS | missing | Kans. | Kansas | Kansas | missing | Kansas, US, United States | missing | کنساس | missing | 2D Polygon | 3.5 | missing | missing | Kansas | missing | US | missing | Kansas | missing | 0 | Kansas | missing | Канзас | missing | missing | USA | missing | missing | missing | Канзас | 1 | State | 4273857 | 1 | 1159315359 | केन्सास | missing |
| 18 | missing | missing | missing | http://en.wikipedia.org/wiki/Missouri | Missouri | missing | United States of America | missing | USA | Missouri | 미주리 | Missouri | United States of America | US.MO | Missouri | missing | Missouri | missing | MO | State | Q1581 | 1 | Missouri | missing | -1 | missing | -92.446 | 1 | missing | Midwest | Missouri | -1 | West North Central | 2 | ميزوري | 7.5 | 密蘇里州 | میزوری | missing | MO | 38.5487 | 20 | Missouri | missing | missing | missing | Missouri | -99 | US.MO | US29 | 2347584 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3531 | মিসৌরি | מיזורי | Missouri | US29 | Μιζούρι | Missouri | missing | 8 | US17 | missing | ミズーリ州 | 1 | missing | 3531 | missing | missing | 1 | 2 | missing | missing | 密苏里州 | 0 | US-MO | missing | Mo. | Missouri | Missouri | missing | Missouri, US, United States | missing | مسوری | missing | 2D Polygon | 3.5 | missing | missing | Missouri | missing | US | US.IL|USA-MOS | Misuri | missing | 0 | Missouri | missing | Миссури | missing | missing | USA | missing | missing | missing | Міссурі | 1 | State | 4398678 | 1 | 1159315361 | मिसौरी | missing |
| 19 | missing | missing | missing | http://en.wikipedia.org/wiki/Nebraska | Nebraska | missing | United States of America | missing | USA | Nebraska | 네브래스카 | Nebraska | United States of America | US.NE | Nebraska | missing | Nebraska | missing | NE|Nebr. | State | Q1553 | 1 | Nebraska | missing | -1 | missing | -99.6855 | 1 | missing | Midwest | Nebraska | -1 | West North Central | 2 | نبراسكا | 7.5 | 內布拉斯加州 | نبراسکا | missing | NE | 41.5002 | 20 | Nebraska | missing | missing | missing | Nebraska | -99 | US.NE | US31 | 2347586 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3532 | নেব্রাস্কা | נברסקה | Nebraska | US31 | Νεμπράσκα | Nebraska | missing | 8 | missing | missing | ネブラスカ州 | 1 | missing | 3532 | missing | missing | 1 | 2 | missing | missing | 內布拉斯加州 | 0 | US-NE | missing | Nebr. | Nebraska | Nebraska | missing | Nebraska, US, United States | missing | نیبراسکا | missing | 2D Polygon | 3.5 | missing | missing | Nebraska | missing | US | missing | Nebraska | missing | 0 | Nebraska | missing | Небраска | missing | missing | USA | missing | missing | missing | Небраска | 1 | State | 5073708 | 1 | 1159315363 | नेब्रास्का | missing |
| 20 | missing | missing | missing | http://en.wikipedia.org/wiki/Oklahoma | Oklahoma | missing | United States of America | missing | USA | Oklahoma | 오클라호마 | Oklahoma | United States of America | US.OK | Oklahoma | missing | Oklahoma | missing | OK|Okla. | State | Q1649 | 1 | Oklahoma | missing | -1 | missing | -97.1309 | 1 | missing | South | Oklahoma | -1 | West South Central | 2 | أوكلاهوما | 7.5 | 奧克拉荷馬州 | اکلاهما | missing | OK | 35.452 | 20 | Oklahoma | missing | missing | missing | Oklahoma | -99 | US.OK | US40 | 2347595 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3533 | ওকলাহোমা | אוקלהומה | Oklahoma | US40 | Οκλαχόμα | Oklahoma | missing | 8 | missing | missing | オクラホマ州 | 1 | missing | 3533 | missing | missing | 1 | 2 | missing | missing | 俄克拉荷马州 | 0 | US-OK | missing | Okla. | Oklahoma | Oklahoma | missing | Oklahoma, US, United States | missing | اوکلاہوما | missing | 2D Polygon | 3.5 | missing | missing | Oklahoma | missing | US | missing | Oklahoma | missing | 0 | Oklahoma | missing | Оклахома | missing | missing | USA | missing | missing | missing | Оклахома | 1 | State | 4544379 | 1 | 1159315365 | ओक्लाहोमा | missing |
| 21 | missing | missing | missing | http://en.wikipedia.org/wiki/South_Dakota | South Dakota | missing | United States of America | missing | USA | Güney Dakota | 사우스다코타 | South Dakota | United States of America | US.SD | South Dakota | missing | Dakota du Sud | missing | SD|S.D. | State | Q1211 | 1 | Dakota do Sul | missing | -1 | missing | -100.255 | 1 | missing | Midwest | South Dakota | -1 | West North Central | 2 | داكوتا الجنوبية | 7.5 | 南達科他州 | داکوتای جنوبی | missing | SD | 44.4711 | 20 | South Dakota | missing | missing | missing | Dél-Dakota | -99 | US.SD | US46 | 2347600 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3534 | দক্ষিণ ডাকোটা | דקוטה הדרומית | South Dakota | US46 | Νότια Ντακότα | South Dakota | missing | 12 | missing | missing | サウスダコタ州 | 1 | missing | 3534 | missing | missing | 1 | 2 | missing | missing | 南达科他州 | 0 | US-SD | missing | S.D. | Nam Dakota | Dakota del Sud | missing | South Dakota, US, United States | missing | جنوبی ڈکوٹا | missing | 2D Polygon | 3.5 | missing | missing | Dakota Południowa | missing | US | missing | Dakota del Sur | missing | 0 | Dakota Selatan | missing | Южная Дакота | missing | missing | USA | missing | missing | missing | Південна Дакота | 1 | State | 5769223 | 1 | 1159315367 | दक्षिण डकोटा | missing |
| 22 | missing | missing | missing | http://en.wikipedia.org/wiki/Louisiana | Louisiana | missing | United States of America | missing | USA | Louisiana | 루이지애나 | Louisiana | United States of America | US.LA | Louisiana | missing | Louisiane | missing | LA | State | Q1588 | 5 | Luisiana | missing | -1 | missing | -91.9991 | 1 | missing | South | Louisiana | -1 | West South Central | 2 | لويزيانا | 7.5 | 路易斯安那州 | لوئیزیانا | missing | LA | 30.5274 | 20 | Louisiana | missing | missing | missing | Louisiana | -99 | US.LA | US22 | 2347577 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3535 | লুইজিয়ানা | לואיזיאנה | Louisiana | US22 | Λουιζιάνα | Louisiana | missing | 9 | missing | missing | ルイジアナ州 | 1 | missing | 3535 | missing | missing | 1 | 2 | missing | missing | 路易斯安那州 | 0 | US-LA | missing | La. | Louisiana | Louisiana | missing | Louisiana, US, United States | missing | لوزیانا | missing | 2D Polygon | 3.5 | missing | missing | Luizjana | missing | US | missing | Luisiana | missing | 0 | Louisiana | missing | Луизиана | missing | missing | USA | missing | missing | missing | Луїзіана | 1 | State | 4331987 | 1 | 1159315221 | लुईज़ियाना | missing |
| 23 | missing | missing | missing | http://en.wikipedia.org/wiki/Texas | Texas | missing | United States of America | missing | USA | Teksas | 텍사스 | Texas | United States of America | US.TX | Texas | missing | Texas | missing | TX|Tex. | State | Q1439 | 4 | Texas | missing | -1 | missing | -98.7607 | 1 | missing | South | Texas | -1 | West South Central | 2 | تكساس | 7.5 | 德克薩斯州 | تگزاس | missing | TX | 31.131 | 20 | Texas | missing | missing | missing | Texas | -99 | US.TX | US48 | 2347602 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3536 | টেক্সাস | טקסס | Texas | US48 | Τέξας | Texas | missing | 5 | missing | missing | テキサス州 | 1 | missing | 3536 | missing | missing | 1 | 2 | missing | missing | 得克萨斯州 | 0 | US-TX | missing | Tex. | Texas | Texas | missing | Texas, US, United States | missing | ٹیکساس | missing | 2D Polygon | 3.5 | missing | missing | Teksas | missing | US | missing | Texas | missing | 0 | Texas | missing | Техас | missing | missing | USA | missing | missing | missing | Техас | 1 | State | 4736286 | 1 | 1159315211 | टॅक्सस | missing |
| 24 | missing | missing | missing | http://en.wikipedia.org/wiki/Connecticut | Connecticut | missing | United States of America | missing | USA | Connecticut | 코네티컷 | Connecticut | United States of America | US.CT | Connecticut | missing | Connecticut | missing | CT|Conn. | State | Q779 | 1 | Connecticut | missing | -1 | missing | -72.7594 | 1 | missing | Northeast | Connecticut | -1 | New England | 2 | كونيتيكت | 7.5 | 康乃狄克州 | کانتیکت | missing | CT | 41.6486 | 20 | Connecticut | missing | missing | missing | Connecticut | -99 | US.CT | US09 | 2347565 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3537 | কানেটিকাট | קונטיקט | Connecticut | US09 | Κονέκτικατ | Connecticut | missing | 11 | missing | missing | コネチカット州 | 1 | missing | 3537 | missing | missing | 1 | 2 | missing | missing | 康涅狄格州 | 0 | US-CT | missing | Conn. | Connecticut | Connecticut | missing | Connecticut, US, United States | missing | کنیکٹیکٹ | missing | 2D Polygon | 3.5 | missing | missing | Connecticut | missing | US | missing | Connecticut | missing | 0 | Connecticut | missing | Коннектикут | missing | missing | USA | missing | missing | missing | Коннектикут | 1 | State | 4831725 | 1 | 1159315301 | कनेक्टिकट | missing |
| 25 | missing | missing | missing | http://en.wikipedia.org/wiki/Massachusetts | Massachusetts | missing | United States of America | missing | USA | Massachusetts | 매사추세츠 | Massachusetts | United States of America | US.MA | Massachusetts | missing | Massachusetts | missing | Commonwealth of Massachusetts|MA|Mass. | State | Q771 | 6 | Massachusetts | missing | -1 | missing | -71.9993 | 1 | missing | Northeast | Massachusetts | -1 | New England | 2 | ماساتشوستس | 7.5 | 麻薩諸塞州 | ماساچوست | missing | MA | 42.3739 | 20 | Massachusetts | missing | missing | missing | Massachusetts | -99 | US.MA | US25 | 2347580 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3513 | ম্যাসাচুসেটস | מסצ'וסטס | Massachusetts | US25 | Μασαχουσέτη | Massachusetts | missing | 13 | missing | missing | マサチューセッツ州 | 1 | missing | 3513 | missing | missing | 1 | 2 | missing | missing | 马萨诸塞州 | 0 | US-MA | missing | Mass. | Massachusetts | Massachusetts | missing | Massachusetts, US, United States | missing | میساچوسٹس | missing | 2D Polygon | 3.5 | missing | missing | Massachusetts | missing | US | missing | Massachusetts | missing | 0 | Massachusetts | missing | Массачусетс | missing | missing | USA | missing | missing | missing | Массачусетс | 1 | State | 6254926 | 1 | 1159312157 | मैसाचूसिट्स | missing |
| 26 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Hampshire | New Hampshire | missing | United States of America | missing | USA | New Hampshire | 뉴햄프셔 | New Hampshire | United States of America | US.NH | New Hampshire | missing | New Hampshire | missing | NH|N.H. | State | Q759 | 1 | Nova Hampshire | missing | -1 | missing | -71.6301 | 1 | missing | Northeast | New Hampshire | -1 | New England | 2 | نيوهامبشير | 7.5 | 新罕布夏州 | نیوهمپشایر | missing | NH | 43.5993 | 20 | New Hampshire | missing | missing | missing | New Hampshire | -99 | US.NH | US33 | 2347588 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3538 | নিউ হ্যাম্প্শায়ার | ניו המפשייר | New Hampshire | US33 | Νιου Χάμσαϊρ | New Hampshire | missing | 13 | missing | missing | ニューハンプシャー州 | 1 | missing | 3538 | missing | missing | 1 | 2 | missing | missing | 新罕布什尔州 | 0 | US-NH | missing | N.H. | New Hampshire | New Hampshire | missing | New Hampshire, US, United States | missing | نیو ہیمپشائر | missing | 2D Polygon | 3.5 | missing | missing | New Hampshire | missing | US | missing | Nuevo Hampshire | missing | 0 | New Hampshire | missing | Нью-Гэмпшир | missing | missing | USA | missing | missing | missing | Нью-Гемпшир | 1 | State | 5090174 | 1 | 1159315303 | नया हेम्पशायर | missing |
| 27 | missing | missing | missing | http://en.wikipedia.org/wiki/Rhode_Island | Rhode Island | missing | United States of America | missing | USA | Rhode Island | 로드아일랜드 | Rhode Island | United States of America | US.RI | Rhode Island | missing | Rhode Island | missing | State of Rhode Island and Providence Plantations|RI|R.I. | State | Q1387 | 6 | Rhode Island | missing | -1 | missing | -71.5082 | 1 | missing | Northeast | Rhode Island | -1 | New England | 2 | رود آيلاند | 7.5 | 羅德島州 | رود آیلند | missing | RI | 41.6242 | 20 | Rhode Island | missing | missing | missing | Rhode Island | -99 | US.RI | US44 | 2347598 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3539 | রোড আইল্যান্ড | רוד איילנד | Rhode Island | US44 | Ρόουντ Άιλαντ | Rhode Island | missing | 12 | missing | missing | ロードアイランド州 | 1 | missing | 3539 | missing | missing | 1 | 2 | missing | missing | 罗得岛州 | 0 | US-RI | missing | R.I. | Rhode Island | Rhode Island | missing | Rhode Island, US, United States | missing | رہوڈ آئی لینڈ | missing | 2D Polygon | 3.5 | missing | missing | Rhode Island | missing | US | missing | Rhode Island | missing | 0 | Rhode Island | missing | Род-Айленд | missing | missing | USA | missing | missing | missing | Род-Айленд | 1 | State | 5224323 | 1 | 1159312213 | रोड आइलैंड | missing |
| 28 | missing | missing | missing | http://en.wikipedia.org/wiki/Vermont | Vermont | missing | United States of America | missing | USA | Vermont | 버몬트 | Vermont | United States of America | US.VT | Vermont | missing | Vermont | missing | VT | State | Q16551 | 1 | Vermont | missing | -1 | missing | -72.7317 | 1 | missing | Northeast | Vermont | -1 | New England | 2 | فيرمونت | 7.5 | 佛蒙特州 | ورمونت | missing | VT | 44.0886 | 20 | Vermont | missing | missing | missing | Vermont | -99 | US.VT | US50 | 2347604 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3540 | ভার্মন্ট | ורמונט | Vermont | US50 | Βερμόντ | Vermont | missing | 7 | missing | missing | バーモント州 | 1 | missing | 3540 | missing | missing | 1 | 2 | missing | missing | 佛蒙特州 | 0 | US-VT | missing | Vt. | Vermont | Vermont | missing | Vermont, US, United States | missing | ورمونٹ | missing | 2D Polygon | 3.5 | missing | missing | Vermont | missing | US | missing | Vermont | missing | 0 | Vermont | missing | Вермонт | missing | missing | USA | missing | missing | missing | Вермонт | 1 | State | 5242283 | 1 | 1159315305 | वर्मांट | missing |
| 29 | missing | missing | missing | http://en.wikipedia.org/wiki/Alabama | Alabama | missing | United States of America | missing | USA | Alabama | 앨라배마 | Alabama | United States of America | US.AL | Alabama | missing | Alabama | missing | AL|Ala. | State | Q173 | 5 | Alabama | missing | -1 | missing | -86.7184 | 1 | missing | South | Alabama | -1 | East South Central | 2 | ألاباما | 7.5 | 阿拉巴馬州 | آلاباما | missing | AL | 32.8551 | 20 | Alabama | missing | missing | missing | Alabama | -99 | US.AL | US01 | 2347559 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3541 | অ্যালাবামা | אלבמה | Alabama | US01 | Αλαμπάμα | Alabama | missing | 7 | missing | missing | アラバマ州 | 1 | missing | 3541 | missing | missing | 1 | 2 | missing | missing | 亚拉巴马州 | 0 | US-AL | missing | Ala. | Alabama | Alabama | missing | Alabama, US, United States | missing | الاباما | missing | 2D Polygon | 3.5 | missing | missing | Alabama | missing | US | missing | Alabama | missing | 0 | Alabama | missing | Алабама | missing | missing | USA | missing | missing | missing | Алабама | 1 | State | 4829764 | 1 | 1159315233 | अलाबामा | missing |
| 30 | missing | missing | missing | http://en.wikipedia.org/wiki/Florida | Florida | missing | United States of America | missing | USA | Florida | 플로리다 | Florida | United States of America | US.FL | Florida | missing | Floride | missing | FL|Fla. | State | Q812 | 5 | Flórida | missing | -1 | missing | -81.6228 | 1 | missing | South | Florida | -1 | South Atlantic | 2 | فلوريدا | 7.5 | 佛羅里達州 | فلوریدا | missing | FL | 28.1568 | 20 | Florida | missing | missing | missing | Florida | -99 | US.FL | US12 | 2347568 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3542 | ফ্লোরিডা | פלורידה | Florida | US12 | Φλόριντα | Florida | missing | 7 | missing | missing | フロリダ州 | 8 | missing | 3542 | missing | missing | 1 | 2 | missing | missing | 佛罗里达州 | 0 | US-FL | missing | Fla. | Florida | Florida | missing | Florida, US, United States | missing | فلوریڈا | missing | 2D Polygon | 3.5 | missing | missing | Floryda | missing | US | missing | Florida | missing | 0 | Florida | missing | Флорида | missing | missing | USA | missing | missing | missing | Флорида | 1 | State | 4155751 | 1 | 1159315207 | फ़्लोरिडा | missing |
| 31 | missing | missing | missing | http://en.wikipedia.org/wiki/Georgia_(U.S._state) | Georgia | missing | United States of America | missing | USA | Georgia | 조지아 | Georgia | United States of America | US.GA | Georgia | missing | Géorgie | missing | GA|Ga. | State | Q1428 | 6 | Geórgia | missing | -1 | missing | -83.4078 | 1 | missing | South | Georgia | -1 | South Atlantic | 2 | جورجيا | 7.5 | 喬治亞州 | جورجیا | missing | GA | 32.8547 | 20 | Georgia | missing | missing | missing | Georgia | -99 | US.GA | US13 | 2347569 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3543 | জর্জিয়া | ג'ורג'יה | Georgia | US13 | Τζόρτζια | Georgia | missing | 7 | missing | missing | ジョージア州 | 1 | missing | 3543 | missing | missing | 1 | 2 | missing | missing | 佐治亚州 | 0 | US-GA | missing | Ga. | Georgia | Georgia | missing | Georgia, US, United States | missing | ریاست جارجیا | missing | 2D Polygon | 3.5 | missing | missing | Georgia | missing | US | missing | Georgia | missing | 0 | Georgia | missing | Джорджия | missing | missing | USA | missing | missing | missing | Джорджія | 1 | State | 4197000 | 1 | 1159311857 | जॉर्जिया | missing |
| 32 | missing | missing | missing | http://en.wikipedia.org/wiki/Mississippi | Mississippi | missing | United States of America | missing | USA | Mississippi | 미시시피 | Mississippi | United States of America | US.MS | Mississippi | missing | Mississippi | missing | MS|Miss. | State | Q1494 | 5 | Mississippi | missing | -1 | missing | -89.7189 | 1 | missing | South | Mississippi | -1 | East South Central | 2 | مسيسيبي | 7.5 | 密西西比州 | میسیسیپی | missing | MS | 32.8657 | 20 | Mississippi | missing | missing | missing | Mississippi | -99 | US.MS | US28 | 2347583 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3544 | মিসিসিপি | מיסיסיפי | Mississippi | US28 | Μισισίπι | Mississippi | missing | 11 | missing | missing | ミシシッピ州 | 1 | missing | 3544 | missing | missing | 1 | 2 | missing | missing | 密西西比州 | 0 | US-MS | missing | Miss. | Mississippi | Mississippi | missing | Mississippi, US, United States | missing | مسیسپی | missing | 2D Polygon | 3.5 | missing | missing | Missisipi | missing | US | missing | Misisipi | missing | 0 | Mississippi | missing | Миссисипи | missing | missing | USA | missing | missing | missing | Міссісіпі | 1 | State | 4436296 | 1 | 1159315231 | मिसिसिप्पी | missing |
| 33 | missing | missing | missing | http://en.wikipedia.org/wiki/South_Carolina | South Carolina | missing | United States of America | missing | USA | Güney Karolina | 사우스캐롤라이나 | South Carolina | United States of America | US.SC | South Carolina | missing | Caroline du Sud | missing | SC|S.C. | State | Q1456 | 1 | Carolina do Sul | missing | -1 | missing | -80.6471 | 1 | missing | South | South Carolina | -1 | South Atlantic | 2 | كارولاينا الجنوبية | 7.5 | 南卡羅萊納州 | کارولینای جنوبی | missing | SC | 33.8578 | 20 | South Carolina | missing | missing | missing | Dél-Karolina | -99 | US.SC | US45 | 2347599 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3545 | সাউথ ক্যারোলাইনা | קרוליינה הדרומית | South Carolina | US45 | Νότια Καρολίνα | South Carolina | missing | 14 | missing | missing | サウスカロライナ州 | 1 | missing | 3545 | missing | missing | 1 | 2 | missing | missing | 南卡罗来纳州 | 0 | US-SC | missing | S.C. | Nam Carolina | Carolina del Sud | missing | South Carolina, US, United States | missing | جنوبی کیرولینا | missing | 2D Polygon | 3.5 | missing | missing | Karolina Południowa | missing | US | missing | Carolina del Sur | missing | 0 | Carolina Selatan | missing | Южная Каролина | missing | missing | USA | missing | missing | missing | Південна Кароліна | 1 | State | 4597040 | 1 | 1159315307 | दक्षिणी केरोलाइना | missing |
| 34 | missing | missing | missing | http://en.wikipedia.org/wiki/Illinois | Illinois | missing | United States of America | missing | USA | Illinois | 일리노이 | Illinois | United States of America | US.IL | Illinois | missing | Illinois | missing | IL|Ill. | State | Q1204 | 1 | Illinois | missing | -1 | missing | -89.1991 | 1 | missing | Midwest | Illinois | -1 | East North Central | 2 | إلينوي | 7.5 | 伊利諾州 | ایلینوی | missing | IL | 39.946 | 20 | Illinois | missing | missing | missing | Illinois | -99 | US.IL | US17 | 2347572 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3546 | ইলিনয় | אילינוי | Illinois | US17 | Ιλινόι | Illinois | missing | 8 | missing | missing | イリノイ州 | 1 | missing | 3546 | missing | missing | 1 | 2 | missing | missing | 伊利诺伊州 | 0 | US-IL | missing | Ill. | Illinois | Illinois | missing | Illinois, US, United States | missing | الینوائے | missing | 2D Polygon | 3.5 | missing | missing | Illinois | missing | US | missing | Illinois | missing | 0 | Illinois | missing | Иллинойс | missing | missing | USA | missing | missing | missing | Іллінойс | 1 | State | 4896861 | 1 | 1159315309 | इलिनॉय | missing |
| 35 | missing | missing | missing | http://en.wikipedia.org/wiki/Indiana | Indiana | missing | United States of America | missing | USA | Indiana | 인디애나 | Indiana | United States of America | US.IN | Indiana | missing | Indiana | missing | IN|Ind. | State | Q1415 | 1 | Indiana | missing | -1 | missing | -86.1396 | 1 | missing | Midwest | Indiana | -1 | East North Central | 2 | إنديانا | 7.5 | 印第安纳州 | ایندیانا | missing | IN | 39.8874 | 20 | Indiana | missing | missing | missing | Indiana | -99 | US.IN | US18 | 2347573 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3547 | ইন্ডিয়ানা | אינדיאנה | Indiana | US18 | Ιντιάνα | Indiana | missing | 7 | missing | missing | インディアナ州 | 1 | missing | 3547 | missing | missing | 1 | 2 | missing | missing | 印第安纳州 | 0 | US-IN | missing | Ind. | Indiana | Indiana | missing | Indiana, US, United States | missing | انڈیانا | missing | 2D Polygon | 3.5 | missing | missing | Indiana | missing | US | missing | Indiana | missing | 0 | Indiana | missing | Индиана | missing | missing | USA | missing | missing | missing | Індіана | 1 | State | 4921868 | 1 | 1159315311 | इंडियाना | missing |
| 36 | missing | missing | missing | http://en.wikipedia.org/wiki/Kentucky | Kentucky | missing | United States of America | missing | USA | Kentucky | 켄터키 | Kentucky | United States of America | US.KY | Kentucky | missing | Kentucky | missing | Commonwealth of Kentucky|KY | State | Q1603 | 1 | Kentucky | missing | -1 | missing | -85.5729 | 1 | missing | South | Kentucky | -1 | East South Central | 2 | كنتاكي | 7.5 | 肯塔基州 | کنتاکی | missing | KY | 37.3994 | 20 | Kentucky | missing | missing | missing | Kentucky | -99 | US.KY | US21 | 2347576 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3548 | কেন্টাকি | קנטקי | Kentucky | US21 | Κεντάκι | Kentucky | missing | 8 | US18 | missing | ケンタッキー州 | 1 | missing | 3548 | missing | missing | 1 | 2 | missing | missing | 肯塔基州 | 0 | US-KY | missing | Ky. | Kentucky | Kentucky | missing | Kentucky, US, United States | missing | کینٹکی | missing | 2D Polygon | 3.5 | missing | missing | Kentucky | missing | US | US.IN|USA-KEN | Kentucky | missing | 0 | Kentucky | missing | Кентукки | missing | missing | USA | missing | missing | missing | Кентуккі | 1 | State | 6254925 | 1 | 1159315313 | केन्टकी | missing |
| 37 | missing | missing | missing | http://en.wikipedia.org/wiki/North_Carolina | North Carolina | missing | United States of America | missing | USA | Kuzey Karolina | 노스캐롤라이나 | North Carolina | United States of America | US.NC | North Carolina | missing | Caroline du Nord | missing | NC|N.C. | State | Q1454 | 5 | Carolina do Norte | missing | -1 | missing | -78.866 | 1 | missing | South | North Carolina | -1 | South Atlantic | 2 | كارولاينا الشمالية | 7.5 | 北卡羅萊納州 | کارولینای شمالی | missing | NC | 35.6152 | 20 | North Carolina | missing | missing | missing | Észak-Karolina | -99 | US.NC | US37 | 2347592 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3549 | নর্থ ক্যারোলাইনা | קרוליינה הצפונית | North Carolina | US37 | Βόρεια Καρολίνα | North Carolina | missing | 14 | missing | missing | ノースカロライナ州 | 1 | missing | 3549 | missing | missing | 1 | 2 | missing | missing | 北卡罗来纳州 | 0 | US-NC | missing | N.C. | Bắc Carolina | Carolina del Nord | missing | North Carolina, US, United States | missing | شمالی کیرولینا | missing | 2D Polygon | 3.5 | missing | missing | Karolina Północna | missing | US | missing | Carolina del Norte | missing | 0 | Carolina Utara | missing | Северная Каролина | missing | missing | USA | missing | missing | missing | Північна Кароліна | 1 | State | 4482348 | 1 | 1159314887 | उत्तरी केरोलिना | missing |
| 38 | missing | missing | missing | http://en.wikipedia.org/wiki/Ohio | Ohio | missing | United States of America | missing | USA | Ohio | 오하이오 | Ohio | United States of America | US.OH | Ohio | missing | Ohio | missing | OH|Ohio | State | Q1397 | 1 | Ohio | missing | -1 | missing | -82.6719 | 1 | missing | Midwest | Ohio | -1 | East North Central | 2 | أوهايو | 7.5 | 俄亥俄州 | اوهایو | missing | OH | 40.0924 | 20 | Ohio | missing | missing | missing | Ohio | -99 | US.OH | US39 | 2347594 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3550 | ওহাইও | אוהיו | Ohio | US39 | Οχάιο | Ohio | missing | 4 | missing | missing | オハイオ州 | 1 | missing | 3550 | missing | missing | 1 | 2 | missing | missing | 俄亥俄州 | 0 | US-OH | missing | Ohio | Ohio | Ohio | missing | Ohio, US, United States | missing | اوہائیو | missing | 2D Polygon | 3.5 | missing | missing | Ohio | missing | US | missing | Ohio | missing | 0 | Ohio | missing | Огайо | missing | missing | USA | missing | missing | missing | Огайо | 1 | State | 5165418 | 1 | 1159315315 | ओहायो | missing |
| 39 | missing | missing | missing | http://en.wikipedia.org/wiki/Tennessee | Tennessee | missing | United States of America | missing | USA | Tennessee | 테네시 | Tennessee | United States of America | US.TN | Tennessee | missing | Tennessee | missing | TN|Tenn. | State | Q1509 | 1 | Tennessee | missing | -1 | missing | -86.3415 | 1 | missing | South | Tennessee | -1 | East South Central | 2 | تينيسي | 7.5 | 田納西州 | تنسی | missing | TN | 35.7514 | 20 | Tennessee | missing | missing | missing | Tennessee | -99 | US.TN | US47 | 2347601 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3551 | টেনেসী | טנסי | Tennessee | US47 | Τενεσί | Tennessee | missing | 9 | missing | missing | テネシー州 | 1 | missing | 3551 | missing | missing | 1 | 2 | missing | missing | 田纳西州 | 0 | US-TN | missing | Tenn. | Tennessee | Tennessee | missing | Tennessee, US, United States | missing | ٹینیسی | missing | 2D Polygon | 3.5 | missing | missing | Tennessee | missing | US | missing | Tennessee | missing | 0 | Tennessee | missing | Теннесси | missing | missing | USA | missing | missing | missing | Теннессі | 1 | State | 4662168 | 1 | 1159315319 | टेनेसी | missing |
| 40 | missing | missing | missing | http://en.wikipedia.org/wiki/Virginia | Virginia | missing | United States of America | missing | USA | Virjinya | 버지니아 | Virginia | United States of America | US.VA | Virginia | missing | Virginie | missing | VA | State | Q1370 | 6 | Virgínia | missing | -1 | missing | -78.2431 | 1 | missing | South | Virginia | -1 | South Atlantic | 2 | فرجينيا | 7.5 | 維吉尼亞州 | ویرجینیا | missing | VA | 37.7403 | 20 | Virginia | missing | missing | missing | Virginia | -99 | US.VA | US51 | 2347605 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3552 | ভার্জিনিয়া | וירג'יניה | Virginia | US51 | Βιρτζίνια | Virginia | missing | 8 | missing | missing | バージニア州 | 1 | missing | 3552 | missing | missing | 1 | 2 | missing | missing | 弗吉尼亚州 | 0 | US-VA | missing | Va. | Virginia | Virginia | missing | Virginia, US, United States | missing | ورجینیا | missing | 2D MultiPolygon | 3.5 | missing | missing | Wirginia | missing | US | missing | Virginia | missing | 0 | Virginia | missing | Виргиния | missing | missing | USA | missing | missing | missing | Вірджинія | 1 | State | 6254928 | 1 | 1159315259 | वर्जीनिया | missing |
| 41 | missing | missing | missing | http://en.wikipedia.org/wiki/Wisconsin | Wisconsin | missing | United States of America | missing | USA | Wisconsin | 위스콘신 | Wisconsin | United States of America | US.WI | Wisconsin | missing | Wisconsin | missing | WI|Wis. | State | Q1537 | 1 | Wisconsin | missing | -1 | missing | -89.5831 | 1 | missing | Midwest | Wisconsin | -1 | East North Central | 2 | ويسكونسن | 7.5 | 威斯康辛州 | ویسکانسین | missing | WI | 44.3709 | 20 | Wisconsin | missing | missing | missing | Wisconsin | -99 | US.WI | US55 | 2347608 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3553 | উইসকনসিন | ויסקונסין | Wisconsin | US55 | Ουισκόνσιν | Wisconsin | missing | 9 | missing | missing | ウィスコンシン州 | 1 | missing | 3553 | missing | missing | 1 | 2 | missing | missing | 威斯康星州 | 0 | US-WI | missing | Wis. | Wisconsin | Wisconsin | missing | Wisconsin, US, United States | missing | وسکونسن | missing | 2D Polygon | 3.5 | missing | missing | Wisconsin | missing | US | missing | Wisconsin | missing | 0 | Wisconsin | missing | Висконсин | missing | missing | USA | missing | missing | missing | Вісконсин | 1 | State | 5279468 | 1 | 1159315321 | विस्कॉन्सिन | missing |
| 42 | missing | missing | missing | http://en.wikipedia.org/wiki/West_Virginia | West Virginia | missing | United States of America | missing | USA | Batı Virginia | 웨스트버지니아 | West Virginia | United States of America | US.WV | West Virginia | missing | Virginie-Occidentale | missing | WV|W.Va. | State | Q1371 | 1 | Virgínia Ocidental | missing | -1 | missing | -80.7128 | 1 | missing | South | West Virginia | -1 | South Atlantic | 2 | فيرجينيا الغربية | 7.5 | 西維吉尼亞州 | ویرجینیای غربی | missing | WV | 38.6422 | 20 | West Virginia | missing | missing | missing | Nyugat-Virginia | -99 | US.WV | US54 | 2347607 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3554 | পশ্চিম ভার্জিনিয়া | וירג'יניה המערבית | West Virginia | US54 | Δυτική Βιρτζίνια | West Virginia | missing | 13 | missing | missing | ウェストバージニア州 | 1 | missing | 3554 | missing | missing | 1 | 2 | missing | missing | 西維吉尼亞州 | 0 | US-WV | missing | W.Va. | Tây Virginia | Virginia Occidentale | missing | West Virginia, US, United States | missing | مغربی ورجینیا | missing | 2D Polygon | 3.5 | missing | missing | Wirginia Zachodnia | missing | US | missing | Virginia Occidental | missing | 0 | Virginia Barat | missing | Западная Виргиния | missing | missing | USA | missing | missing | missing | Західна Вірджинія | 1 | State | 4826850 | 1 | 1159315323 | पश्चिमी वर्जीनिया | missing |
| 43 | missing | missing | missing | http://en.wikipedia.org/wiki/Delaware | Delaware | missing | United States of America | missing | USA | Delaware | 델라웨어 | Delaware | United States of America | US.DE | Delaware | missing | Delaware | missing | DE|Del. | State | Q1393 | 1 | Delaware | missing | -1 | missing | -75.4112 | 1 | missing | South | Delaware | -1 | South Atlantic | 2 | ديلاوير | 7.5 | 特拉華州 | دلاویر | missing | DE | 38.8657 | 20 | Delaware | missing | missing | missing | Delaware | -99 | US.DE | US10 | 2347566 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3555 | ডেলাওয়্যার | דלאוור | Delaware | US10 | Ντέλαγουερ | Delaware | missing | 8 | missing | missing | デラウェア州 | 1 | missing | 3555 | missing | missing | 1 | 2 | missing | missing | 特拉华州 | 0 | US-DE | missing | Del. | Delaware | Delaware | missing | Delaware, US, United States | missing | ڈیلاویئر | missing | 2D Polygon | 3.5 | missing | missing | Delaware | missing | US | missing | Delaware | missing | 0 | Delaware | missing | Делавэр | missing | missing | USA | missing | missing | missing | Делавер | 1 | State | 4142224 | 1 | 1159315325 | डेलावेयर | missing |
| 44 | missing | missing | missing | http://en.wikipedia.org/wiki/Washington,_D.C. | Washington | missing | United States of America | missing | USA | Washington | 워싱턴 D.C. | District of Columbia | United States of America | US.DC | Washington D.C. | missing | Washington | missing | DC|D.C. | Federal District | Q61 | 1 | Washington | missing | -1 | missing | -77.0113 | 1 | missing | South | District of Columbia | -1 | South Atlantic | 2 | واشنطن | 7.5 | 華盛頓哥倫比亞特區 | واشینگتن، دی. سی. | missing | DC | 38.8922 | 20 | Washington | missing | missing | missing | Washington | 9 | US.DC | US11 | 2347567 | missing | missing | 9 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3556 | ওয়াশিংটন | וושינגטון די. סי. | Washington | US11 | Ουάσινγκτον | District of Columbia | missing | 20 | missing | missing | ワシントンD.C. | 1 | missing | 3556 | missing | missing | 1 | 2 | missing | missing | 华盛顿哥伦比亚特区 | 0 | US-DC | missing | D.C. | Washington | Washington | missing | District of Columbia, US, United States | missing | واشنگٹن ڈی سی | missing | 2D Polygon | 3.5 | missing | missing | Waszyngton | missing | US | missing | Washington D. C. | missing | 0 | Washington | missing | Вашингтон | missing | missing | USA | missing | missing | missing | Вашингтон | 1 | Federal District | 4138106 | 1 | 1159315327 | वॉशिंगटन डी॰ सी॰ | missing |
| 45 | missing | missing | missing | http://en.wikipedia.org/wiki/Maryland | Maryland | missing | United States of America | missing | USA | Maryland | 메릴랜드 | Maryland | United States of America | US.MD | Maryland | missing | Maryland | missing | MD | State | Q1391 | 1 | Maryland | missing | -1 | missing | -77.0454 | 1 | missing | South | Maryland | -1 | South Atlantic | 2 | ماريلند | 7.5 | 馬里蘭州 | مریلند | missing | MD | 39.3874 | 20 | Maryland | missing | missing | missing | Maryland | -99 | US.MD | US24 | 2347579 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3557 | মেরিল্যান্ড | מרילנד | Maryland | US24 | Μέριλαντ | Maryland | missing | 8 | missing | missing | メリーランド州 | 1 | missing | 3557 | missing | missing | 1 | 2 | missing | missing | 马里兰州 | 0 | US-MD | missing | Md. | Maryland | Maryland | missing | Maryland, US, United States | missing | میری لینڈ | missing | 2D Polygon | 3.5 | missing | missing | Maryland | missing | US | missing | Maryland | missing | 0 | Maryland | missing | Мэриленд | missing | missing | USA | missing | missing | missing | Меріленд | 1 | State | 4361885 | 1 | 1159315329 | मैरीलैंड | missing |
| 46 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Jersey | New Jersey | missing | United States of America | missing | USA | New Jersey | 뉴저지 | New Jersey | United States of America | US.NJ | New Jersey | missing | New Jersey | missing | NJ|N.J. | State | Q1408 | 5 | Nova Jérsia | missing | -1 | missing | -74.4653 | 1 | missing | Northeast | New Jersey | -1 | Middle Atlantic | 2 | نيوجيرسي | 7.5 | 紐澤西州 | نیوجرسی | missing | NJ | 40.0449 | 20 | New Jersey | missing | missing | missing | New Jersey | -99 | US.NJ | US34 | 2347589 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3558 | নিউ জার্সি | ניו ג'רזי | New Jersey | US34 | Νιου Τζέρσεϊ | New Jersey | missing | 10 | missing | missing | ニュージャージー州 | 1 | missing | 3558 | missing | missing | 1 | 2 | missing | missing | 新泽西州 | 0 | US-NJ | missing | N.J. | New Jersey | New Jersey | missing | New Jersey, US, United States | missing | نیو جرسی | missing | 2D Polygon | 3.5 | missing | missing | New Jersey | missing | US | missing | Nueva Jersey | missing | 0 | New Jersey | missing | Нью-Джерси | missing | missing | USA | missing | missing | missing | Нью-Джерсі | 1 | State | 5101760 | 1 | 1159315267 | न्यू जर्सी | missing |
| 47 | missing | missing | missing | http://en.wikipedia.org/wiki/New_York | New York | missing | United States of America | missing | USA | New York | 뉴욕 | New York | United States of America | US.NY | New York | missing | État de New York | missing | NY|N.Y. | State | Q1384 | 3 | Nova Iorque | missing | -1 | missing | -75.3242 | 1 | missing | Northeast | New York | -1 | Middle Atlantic | 2 | نيويورك | 7.5 | 紐約州 | نیویورک | missing | NY | 43.1988 | 20 | New York | missing | missing | missing | New York | -99 | US.NY | US36 | 2347591 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3559 | নিউ ইয়র্ক | ניו יורק | New York | US36 | Νέα Υόρκη | New York | missing | 8 | missing | missing | ニューヨーク州 | 1 | missing | 3559 | missing | missing | 1 | 2 | missing | missing | 纽约州 | 0 | US-NY | missing | N.Y. | New York | New York | missing | New York, US, United States | missing | نیویارک | missing | 2D Polygon | 3.5 | missing | missing | Nowy Jork | missing | US | missing | Nueva York | missing | 0 | New York | missing | Нью-Йорк | missing | missing | USA | missing | missing | missing | штат Нью-Йорк | 1 | State | 5128638 | 1 | 1159312155 | न्यूयॉर्क | missing |
| 48 | missing | missing | missing | http://en.wikipedia.org/wiki/Pennsylvania | Pennsylvania | missing | United States of America | missing | USA | Pensilvanya | 펜실베이니아 | Pennsylvania | United States of America | US.PA | Pennsylvania | missing | Pennsylvanie | missing | Commonwealth of Pennsylvania|PA | State | Q1400 | 1 | Pensilvânia | missing | -1 | missing | -77.6094 | 1 | missing | Northeast | Pennsylvania | -1 | Middle Atlantic | 2 | بنسيلفانيا | 7.5 | 賓夕法尼亞州 | پنسیلوانیا | missing | PA | 40.8601 | 20 | Pennsylvania | missing | missing | missing | Pennsylvania | -99 | US.PA | US42 | 2347597 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3560 | পেনসিলভেনিয়া | פנסילבניה | Pennsylvania | US42 | Πενσιλβάνια | Pennsylvania | missing | 12 | missing | missing | ペンシルベニア州 | 1 | missing | 3560 | missing | missing | 1 | 2 | missing | missing | 宾夕法尼亚州 | 0 | US-PA | missing | Pa. | Pennsylvania | Pennsylvania | missing | Pennsylvania, US, United States | missing | پنسلوانیا | missing | 2D Polygon | 3.5 | missing | missing | Pensylwania | missing | US | missing | Pensilvania | missing | 0 | Pennsylvania | missing | Пенсильвания | missing | missing | USA | missing | missing | missing | Пенсильванія | 1 | State | 6254927 | 1 | 1159315331 | पेन्सिलवेनिया | missing |
| 49 | missing | missing | missing | http://en.wikipedia.org/wiki/Maine | Maine | missing | United States of America | missing | USA | Maine | 메인 | Maine | United States of America | US.ME | Maine | missing | Maine | missing | ME|Maine | State | Q724 | 6 | Maine | missing | -1 | missing | -69.1973 | 1 | missing | Northeast | Maine | -1 | New England | 2 | مين | 7.5 | 缅因州 | مین | missing | ME | 45.148 | 20 | Maine | missing | missing | missing | Maine | -99 | US.ME | US23 | 2347578 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3561 | মেইন | מיין | Maine | US23 | Μέιν | Maine | missing | 5 | missing | missing | メイン州 | 1 | missing | 3561 | missing | missing | 1 | 2 | missing | missing | 缅因州 | 0 | US-ME | missing | Maine | Maine | Maine | missing | Maine, US, United States | missing | مینے | missing | 2D Polygon | 3.5 | missing | missing | Maine | missing | US | missing | Maine | missing | 0 | Maine | missing | Мэн | missing | missing | USA | missing | missing | missing | Мен | 1 | State | 4971068 | 1 | 1159308501 | मेन | missing |
| 50 | missing | missing | missing | http://en.wikipedia.org/wiki/Michigan | Michigan | missing | United States of America | missing | USA | Michigan | 미시간 | Michigan | United States of America | US.MI | Michigan | missing | Michigan | missing | MI|Mich. | State | Q1166 | 1 | Michigan | missing | -1 | missing | -84.9479 | 1 | missing | Midwest | Michigan | -1 | East North Central | 2 | ميشيغان | 7.5 | 密歇根州 | میشیگان | missing | MI | 43.4343 | 20 | Michigan | missing | missing | missing | Michigan | -99 | US.MI | US26 | 2347581 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3562 | মিশিগান | מישיגן | Michigan | US26 | Μίσιγκαν | Michigan | missing | 8 | missing | missing | ミシガン州 | 1 | missing | 3562 | missing | missing | 1 | 2 | missing | missing | 密歇根州 | 0 | US-MI | missing | Mich. | Michigan | Michigan | missing | Michigan, US, United States | missing | مشی گن | missing | 2D Polygon | 3.5 | missing | missing | Michigan | missing | US | missing | Míchigan | missing | 0 | Michigan | missing | Мичиган | missing | missing | USA | missing | missing | missing | Мічиган | 1 | State | 5001836 | 1 | 1159314665 | मिशिगन | missing |
| 51 | missing | missing | missing | http://en.wikipedia.org/wiki/Alaska | Alaska | missing | United States of America | missing | USA | Alaska | 알래스카 | Alaska | United States of America | US.AK | Alaska | missing | Alaska | missing | AK|Alaska | State | Q797 | 6 | Alasca | missing | -1 | missing | -151.604 | 1 | missing | West | Alaska | -1 | Pacific | 2 | ألاسكا | 7.5 | 阿拉斯加州 | آلاسکا | missing | AK | 65.3609 | 20 | Alaska | missing | missing | missing | Alaszka | -99 | US.AK | US02 | 2347560 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3563 | আলাস্কা | אלסקה | Alaska | US02 | Αλάσκα | Alaska | missing | 6 | missing | missing | アラスカ州 | 1 | missing | 3563 | missing | missing | 1 | 2 | missing | missing | 阿拉斯加州 | 0 | US-AK | missing | Alaska | Alaska | Alaska | missing | Alaska, US, United States | missing | الاسکا | missing | 2D MultiPolygon | 3.5 | missing | missing | Alaska | missing | US | missing | Alaska | missing | 0 | Alaska | missing | Аляска | missing | missing | USA | missing | missing | missing | Аляска | 1 | State | 5879092 | 1 | 1159308731 | अलास्का | missing |
First, filter out everything that's not in the USA:
filter!(:gu_a3 => ==("USA"), admin_1_df)| Row | FCLASS_IL | FCLASS_US | FCLASS_AR | wikipedia | name_en | FCLASS_FR | admin | gns_lang | gu_a3 | name_tr | name_ko | name | geonunit | gn_a1_code | name_nl | FCLASS_JP | name_fr | FCLASS_SE | name_alt | type_en | wikidataid | adm0_sr | name_pt | FCLASS_TLC | gns_id | sub_code | longitude | mapcolor13 | gns_region | region | gn_name | gns_level | region_sub | scalerank | name_ar | max_label | name_zht | name_fa | FCLASS_PL | postal | latitude | check_me | name_sv | FCLASS_IN | FCLASS_BR | FCLASS_UA | name_hu | sameascity | code_hasc | code_local | woe_id | FCLASS_BD | FCLASS_GB | labelrank | sov_a3 | FCLASS_PT | FCLASS_KO | FCLASS_NP | featurecla | min_zoom | gns_adm1 | adm1_code | name_bn | name_he | name_de | fips | name_el | woe_name | FCLASS_MA | name_len | fips_alt | FCLASS_PS | name_ja | datarank | FCLASS_ISO | diss_me | region_cod | gns_name | mapcolor9 | adm0_label | FCLASS_TR | FCLASS_SA | name_zh | area_sqkm | iso_3166_2 | name_local | abbrev | name_vi | name_it | FCLASS_DE | woe_label | FCLASS_VN | name_ur | FCLASS_IT | geometry | min_label | gn_region | note | name_pl | FCLASS_ES | iso_a2 | hasc_maybe | name_es | FCLASS_CN | provnum_ne | name_id | FCLASS_TW | name_ru | FCLASS_EG | FCLASS_GR | adm0_a3 | FCLASS_ID | FCLASS_NL | FCLASS_PK | name_uk | gadm_level | type | gn_id | gn_level | ne_id | name_hi | FCLASS_RU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Missing | Missing | Missing | String | String | Missing | String | Missing | String | String | String | String | String | String | String | Missing | String | Missing | String | String | String | Int64 | String | Missing | Int64 | Missing | Float64 | Int64 | Missing | String | String | Int64 | String | Int64 | String | Float64 | String | String | Missing | String | Float64 | Int64 | String | Missing | Missing | Missing | String | Int64 | String | String | Int64 | Missing | Missing | Int64 | String | Missing | Missing | Missing | String | Int64 | Missing | String | String | String | String | String | String | String | Missing | Int64 | String? | Missing | String | Int64 | Missing | Int64 | Missing | Missing | Int64 | Int64 | Missing | Missing | String | Int64 | String | Missing | String | String | String | Missing | String | Missing | String | Missing | Union… | Float64 | Missing | Missing | String | Missing | String | String? | String | Missing | Int64 | String | Missing | String | Missing | Missing | String | Missing | Missing | Missing | String | Int64 | String | Int64 | Int64 | Int64 | String | Missing | |
| 1 | missing | missing | missing | http://en.wikipedia.org/wiki/Minnesota | Minnesota | missing | United States of America | missing | USA | Minnesota | 미네소타 | Minnesota | United States of America | US.MN | Minnesota | missing | Minnesota | missing | MN|Minn. | State | Q1527 | 1 | Minnesota | missing | -1 | missing | -93.364 | 1 | missing | Midwest | Minnesota | -1 | West North Central | 2 | مينيسوتا | 7.5 | 明尼蘇達州 | مینهسوتا | missing | MN | 46.0592 | 20 | Minnesota | missing | missing | missing | Minnesota | -99 | US.MN | US27 | 2347582 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3514 | মিনেসোটা | מינסוטה | Minnesota | US27 | Μινεσότα | Minnesota | missing | 9 | missing | missing | ミネソタ州 | 1 | missing | 3514 | missing | missing | 1 | 2 | missing | missing | 明尼苏达州 | 0 | US-MN | missing | Minn. | Minnesota | Minnesota | missing | Minnesota, US, United States | missing | مینیسوٹا | missing | 2D Polygon | 3.5 | missing | missing | Minnesota | missing | US | missing | Minnesota | missing | 0 | Minnesota | missing | Миннесота | missing | missing | USA | missing | missing | missing | Міннесота | 1 | State | 5037779 | 1 | 1159315297 | मिनेसोटा | missing |
| 2 | missing | missing | missing | http://en.wikipedia.org/wiki/Montana | Montana | missing | United States of America | missing | USA | Montana | 몬태나 | Montana | United States of America | US.MT | Montana | missing | Montana | missing | MT|Mont. | State | Q1212 | 1 | Montana | missing | -1 | missing | -110.044 | 1 | missing | West | Montana | -1 | Mountain | 2 | مونتانا | 7.5 | 蒙大拿州 | ایالت مونتانا | missing | MT | 46.9965 | 20 | Montana | missing | missing | missing | Montana | -99 | US.MT | US30 | 2347585 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3515 | মন্টানা | מונטנה | Montana | US30 | Μοντάνα | Montana | missing | 7 | missing | missing | モンタナ州 | 1 | missing | 3515 | missing | missing | 1 | 2 | missing | missing | 蒙大拿州 | 0 | US-MT | missing | Mont. | Montana | Montana | missing | Montana, US, United States | missing | مونٹانا | missing | 2D Polygon | 3.5 | missing | missing | Montana | missing | US | missing | Montana | missing | 0 | Montana | missing | Монтана | missing | missing | USA | missing | missing | missing | Монтана | 1 | State | 5667009 | 1 | 1159315333 | मोन्टाना | missing |
| 3 | missing | missing | missing | http://en.wikipedia.org/wiki/North_Dakota | North Dakota | missing | United States of America | missing | USA | Kuzey Dakota | 노스다코타 | North Dakota | United States of America | US.ND | Noord-Dakota | missing | Dakota du Nord | missing | ND|N.D. | State | Q1207 | 1 | Dakota do Norte | missing | -1 | missing | -100.302 | 1 | missing | Midwest | North Dakota | -1 | West North Central | 2 | داكوتا الشمالية | 7.5 | 北達科他州 | داکوتای شمالی | missing | ND | 47.4675 | 20 | North Dakota | missing | missing | missing | Észak-Dakota | -99 | US.ND | US38 | 2347593 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3516 | নর্থ ডাকোটা | דקוטה הצפונית | North Dakota | US38 | Βόρεια Ντακότα | North Dakota | missing | 12 | missing | missing | ノースダコタ州 | 1 | missing | 3516 | missing | missing | 1 | 2 | missing | missing | 北达科他州 | 0 | US-ND | missing | N.D. | Bắc Dakota | Dakota del Nord | missing | North Dakota, US, United States | missing | شمالی ڈکوٹا | missing | 2D Polygon | 3.5 | missing | missing | Dakota Północna | missing | US | missing | Dakota del Norte | missing | 0 | Dakota Utara | missing | Северная Дакота | missing | missing | USA | missing | missing | missing | Північна Дакота | 1 | State | 5690763 | 1 | 1159315337 | उत्तर डेकोटा | missing |
| 4 | missing | missing | missing | http://en.wikipedia.org/wiki/Hawaii | Hawaii | missing | United States of America | missing | USA | Hawaii | 하와이 | Hawaii | United States of America | US.HI | Hawaï | missing | Hawaï | missing | HI|Hawaii | State | Q782 | 8 | Havaí | missing | -1 | missing | -157.999 | 1 | missing | West | Hawaii | -1 | Pacific | 2 | هاواي | 7.5 | 夏威夷州 | هاوائی | missing | HI | 21.4919 | 20 | Hawaii | missing | missing | missing | Hawaii | -99 | US.HI | US15 | 2347570 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3517 | হাওয়াই | הוואי | Hawaii | US15 | Χαβάη | Hawaii | missing | 6 | missing | missing | ハワイ州 | 1 | missing | 3517 | missing | missing | 1 | 2 | missing | missing | 夏威夷州 | 0 | US-HI | missing | Hawaii | Hawaii | Hawaii | missing | Hawaii, US, United States | missing | ہوائی | missing | 2D MultiPolygon | 3.5 | missing | missing | Hawaje | missing | US | missing | Hawái | missing | 0 | Hawaii | missing | Гавайи | missing | missing | USA | missing | missing | missing | Гаваї | 1 | State | 5855797 | 1 | 1159308409 | हवाई | missing |
| 5 | missing | missing | missing | http://en.wikipedia.org/wiki/Idaho | Idaho | missing | United States of America | missing | USA | Idaho | 아이다호 | Idaho | United States of America | US.ID | Idaho | missing | Idaho | missing | ID|Idaho | State | Q1221 | 1 | Idaho | missing | -1 | missing | -114.133 | 1 | missing | West | Idaho | -1 | Mountain | 2 | أيداهو | 7.5 | 愛達荷州 | آیداهو | missing | ID | 43.7825 | 20 | Idaho | missing | missing | missing | Idaho | -99 | US.ID | US16 | 2347571 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3518 | আইডাহো | איידהו | Idaho | US16 | Άινταχο | Idaho | missing | 5 | missing | missing | アイダホ州 | 1 | missing | 3518 | missing | missing | 1 | 2 | missing | missing | 爱达荷州 | 0 | US-ID | missing | Idaho | Idaho | Idaho | missing | Idaho, US, United States | missing | ایڈاہو | missing | 2D Polygon | 3.5 | missing | missing | Idaho | missing | US | missing | Idaho | missing | 0 | Idaho | missing | Айдахо | missing | missing | USA | missing | missing | missing | Айдахо | 1 | State | 5596512 | 1 | 1159315339 | आयडाहो | missing |
| 6 | missing | missing | missing | http://en.wikipedia.org/wiki/Washington_(state) | Washington | missing | United States of America | missing | USA | Vaşington | 워싱턴 | Washington | United States of America | US.WA | Washington | missing | Washington | missing | WA|Wash. | State | Q1223 | 6 | Washington | missing | -1 | missing | -120.361 | 1 | missing | West | Washington | -1 | Pacific | 2 | واشنطن | 7.5 | 華盛頓州 | ایالت واشینگتن | missing | WA | 47.4865 | 20 | Washington | missing | missing | missing | Washington | -99 | US.WA | US53 | 2347606 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3519 | ওয়াশিংটন | וושינגטון | Washington | US53 | Ουάσινγκτον | Washington | missing | 10 | missing | missing | ワシントン州 | 1 | missing | 3519 | missing | missing | 1 | 2 | missing | missing | 华盛顿州 | 0 | US-WA | missing | Wash. | Washington | Washington | missing | Washington, US, United States | missing | ریاست واشنگٹن | missing | 2D Polygon | 3.5 | missing | missing | Waszyngton | missing | US | missing | Washington | missing | 0 | Washington | missing | Вашингтон | missing | missing | USA | missing | missing | missing | Вашингтон | 1 | State | 5815135 | 1 | 1159309547 | वॉशिंगटन राज्य | missing |
| 7 | missing | missing | missing | http://en.wikipedia.org/wiki/Arizona | Arizona | missing | United States of America | missing | USA | Arizona | 애리조나 | Arizona | United States of America | US.AZ | Arizona | missing | Arizona | missing | AZ|Ariz. | State | Q816 | 1 | Arizona | missing | -1 | missing | -111.935 | 1 | missing | West | Arizona | -1 | Mountain | 2 | أريزونا | 7.5 | 亞利桑那州 | آریزونا | missing | AZ | 34.3046 | 20 | Arizona | missing | missing | missing | Arizona | -99 | US.AZ | US04 | 2347561 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3520 | অ্যারিজোনা | אריזונה | Arizona | US04 | Αριζόνα | Arizona | missing | 7 | missing | missing | アリゾナ州 | 1 | missing | 3520 | missing | missing | 1 | 2 | missing | missing | 亚利桑那州 | 0 | US-AZ | missing | Ariz. | Arizona | Arizona | missing | Arizona, US, United States | missing | ایریزونا | missing | 2D Polygon | 3.5 | missing | missing | Arizona | missing | US | missing | Arizona | missing | 0 | Arizona | missing | Аризона | missing | missing | USA | missing | missing | missing | Аризона | 1 | State | 5551752 | 1 | 1159315341 | एरीजोना | missing |
| 8 | missing | missing | missing | http://en.wikipedia.org/wiki/California | California | missing | United States of America | missing | USA | Kaliforniya | 캘리포니아 | California | United States of America | US.CA | Californië | missing | Californie | missing | CA|Calif. | State | Q99 | 8 | Califórnia | missing | -1 | missing | -119.591 | 1 | missing | West | California | -1 | Pacific | 2 | كاليفورنيا | 7.5 | 加利福尼亞州 | کالیفرنیا | missing | CA | 36.7496 | 20 | Kalifornien | missing | missing | missing | Kalifornia | -99 | US.CA | US06 | 2347563 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3521 | ক্যালিফোর্নিয়া | קליפורניה | Kalifornien | US06 | Καλιφόρνια | California | missing | 10 | missing | missing | カリフォルニア州 | 1 | missing | 3521 | missing | missing | 1 | 2 | missing | missing | 加利福尼亚州 | 0 | US-CA | missing | Calif. | California | California | missing | California, US, United States | missing | کیلی فورنیا | missing | 2D Polygon | 3.5 | missing | missing | Kalifornia | missing | US | missing | California | missing | 0 | California | missing | Калифорния | missing | missing | USA | missing | missing | missing | Каліфорнія | 1 | State | 5332921 | 1 | 1159308415 | कैलिफ़ोर्निया | missing |
| 9 | missing | missing | missing | http://en.wikipedia.org/wiki/Colorado | Colorado | missing | United States of America | missing | USA | Colorado | 콜로라도 | Colorado | United States of America | US.CO | Colorado | missing | Colorado | missing | CO|Colo. | State | Q1261 | 1 | Colorado | missing | -1 | missing | -105.543 | 1 | missing | West | Colorado | -1 | Mountain | 2 | كولورادو | 7.5 | 科羅拉多州 | کلرادو | missing | CO | 38.9998 | 20 | Colorado | missing | missing | missing | Colorado | -99 | US.CO | US08 | 2347564 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3522 | কলোরাডো | קולורדו | Colorado | US08 | Κολοράντο | Colorado | missing | 8 | missing | missing | コロラド州 | 1 | missing | 3522 | missing | missing | 1 | 2 | missing | missing | 科罗拉多州 | 0 | US-CO | missing | Colo. | Colorado | Colorado | missing | Colorado, US, United States | missing | کولوراڈو | missing | 2D Polygon | 3.5 | missing | missing | Kolorado | missing | US | missing | Colorado | missing | 0 | Colorado | missing | Колорадо | missing | missing | USA | missing | missing | missing | Колорадо | 1 | State | 5417618 | 1 | 1159315343 | कॉलराडो | missing |
| 10 | missing | missing | missing | http://en.wikipedia.org/wiki/Nevada | Nevada | missing | United States of America | missing | USA | Nevada | 네바다 | Nevada | United States of America | US.NV | Nevada | missing | Nevada | missing | NV|Nev. | State | Q1227 | 1 | Nevada | missing | -1 | missing | -117.02 | 1 | missing | West | Nevada | -1 | Mountain | 2 | نيفادا | 7.5 | 內華達州 | نوادا | missing | NV | 39.4299 | 20 | Nevada | missing | missing | missing | Nevada | -99 | US.NV | US32 | 2347587 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3523 | নেভাডা | נבדה | Nevada | US32 | Νεβάδα | Nevada | missing | 6 | missing | missing | ネバダ州 | 1 | missing | 3523 | missing | missing | 1 | 2 | missing | missing | 内华达州 | 0 | US-NV | missing | Nev. | Nevada | Nevada | missing | Nevada, US, United States | missing | نیواڈا | missing | 2D Polygon | 3.5 | missing | missing | Nevada | missing | US | missing | Nevada | missing | 0 | Nevada | missing | Невада | missing | missing | USA | missing | missing | missing | Невада | 1 | State | 5509151 | 1 | 1159315345 | नेवाडा | missing |
| 11 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Mexico | New Mexico | missing | United States of America | missing | USA | New Mexico | 뉴멕시코 | New Mexico | United States of America | US.NM | New Mexico | missing | Nouveau-Mexique | missing | NM|N.M. | State | Q1522 | 1 | Novo México | missing | -1 | missing | -106.024 | 1 | missing | West | New Mexico | -1 | Mountain | 2 | نيومكسيكو | 7.5 | 新墨西哥州 | نیومکزیکو | missing | NM | 34.5002 | 20 | New Mexico | missing | missing | missing | Új-Mexikó | -99 | US.NM | US35 | 2347590 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3524 | নিউ মেক্সিকো | ניו מקסיקו | New Mexico | US35 | Νέο Μεξικό | New Mexico | missing | 10 | missing | missing | ニューメキシコ州 | 1 | missing | 3524 | missing | missing | 1 | 2 | missing | missing | 新墨西哥州 | 0 | US-NM | missing | N.M. | New Mexico | Nuovo Messico | missing | New Mexico, US, United States | missing | نیو میکسیکو | missing | 2D Polygon | 3.5 | missing | missing | Nowy Meksyk | missing | US | missing | Nuevo México | missing | 0 | New Mexico | missing | Нью-Мексико | missing | missing | USA | missing | missing | missing | Нью-Мексико | 1 | State | 5481136 | 1 | 1159315347 | नया मेक्सिको | missing |
| 12 | missing | missing | missing | http://en.wikipedia.org/wiki/Oregon | Oregon | missing | United States of America | missing | USA | Oregon | 오리건 | Oregon | United States of America | US.OR | Oregon | missing | Oregon | missing | OR|Ore. | State | Q824 | 6 | Oregon | missing | -1 | missing | -120.386 | 1 | missing | West | Oregon | -1 | Pacific | 2 | أوريغون | 7.5 | 奧勒岡州 | اورگن | missing | OR | 43.8333 | 20 | Oregon | missing | missing | missing | Oregon | -99 | US.OR | US41 | 2347596 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3525 | অরেগন | אורגון | Oregon | US41 | Όρεγκον | Oregon | missing | 6 | missing | missing | オレゴン州 | 1 | missing | 3525 | missing | missing | 1 | 2 | missing | missing | 俄勒冈州 | 0 | US-OR | missing | Ore. | Oregon | Oregon | missing | Oregon, US, United States | missing | اوریگون | missing | 2D Polygon | 3.5 | missing | missing | Oregon | missing | US | missing | Oregón | missing | 0 | Oregon | missing | Орегон | missing | missing | USA | missing | missing | missing | Орегон | 1 | State | 5744337 | 1 | 1159309549 | औरिगन | missing |
| 13 | missing | missing | missing | http://en.wikipedia.org/wiki/Utah | Utah | missing | United States of America | missing | USA | Utah | 유타 | Utah | United States of America | US.UT | Utah | missing | Utah | missing | UT | State | Q829 | 1 | Utah | missing | -1 | missing | -111.544 | 1 | missing | West | Utah | -1 | Mountain | 2 | يوتا | 7.5 | 猶他州 | یوتا | missing | UT | 39.5007 | 20 | Utah | missing | missing | missing | Utah | -99 | US.UT | US49 | 2347603 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3526 | ইউটা | יוטה | Utah | US49 | Γιούτα | Utah | missing | 4 | missing | missing | ユタ州 | 1 | missing | 3526 | missing | missing | 1 | 2 | missing | missing | 犹他州 | 0 | US-UT | missing | Utah | Utah | Utah | missing | Utah, US, United States | missing | یوٹاہ | missing | 2D Polygon | 3.5 | missing | missing | Utah | missing | US | missing | Utah | missing | 0 | Utah | missing | Юта | missing | missing | USA | missing | missing | missing | Юта | 1 | State | 5549030 | 1 | 1159315349 | यूटाह | missing |
| 14 | missing | missing | missing | http://en.wikipedia.org/wiki/Wyoming | Wyoming | missing | United States of America | missing | USA | Wyoming | 와이오밍 | Wyoming | United States of America | US.WY | Wyoming | missing | Wyoming | missing | WY|Wyo. | State | Q1214 | 1 | Wyoming | missing | -1 | missing | -107.552 | 1 | missing | West | Wyoming | -1 | Mountain | 2 | وايومنغ | 7.5 | 懷俄明州 | وایومینگ | missing | WY | 42.9999 | 20 | Wyoming | missing | missing | missing | Wyoming | -99 | US.WY | US56 | 2347609 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3527 | ওয়াইয়োমিং | ויומינג | Wyoming | US56 | Ουαϊόμινγκ | Wyoming | missing | 7 | missing | missing | ワイオミング州 | 1 | missing | 3527 | missing | missing | 1 | 2 | missing | missing | 怀俄明州 | 0 | US-WY | missing | Wyo. | Wyoming | Wyoming | missing | Wyoming, US, United States | missing | وائیومنگ | missing | 2D Polygon | 3.5 | missing | missing | Wyoming | missing | US | missing | Wyoming | missing | 0 | Wyoming | missing | Вайоминг | missing | missing | USA | missing | missing | missing | Вайомінг | 1 | State | 5843591 | 1 | 1159315351 | वायोमिंग | missing |
| 15 | missing | missing | missing | http://en.wikipedia.org/wiki/Arkansas | Arkansas | missing | United States of America | missing | USA | Arkansas | 아칸소 | Arkansas | United States of America | US.AR | Arkansas | missing | Arkansas | missing | AR|Ark. | State | Q1612 | 1 | Arkansas | missing | -1 | missing | -92.1428 | 1 | missing | South | Arkansas | -1 | West South Central | 2 | أركنساس | 7.5 | 阿肯色州 | آرکانزاس | missing | AR | 34.7563 | 20 | Arkansas | missing | missing | missing | Arkansas | -99 | US.AR | US05 | 2347562 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3528 | আর্কানসাস | ארקנסו | Arkansas | US05 | Άρκανσο | Arkansas | missing | 8 | missing | missing | アーカンソー州 | 1 | missing | 3528 | missing | missing | 1 | 2 | missing | missing | 阿肯色州 | 0 | US-AR | missing | Ark. | Arkansas | Arkansas | missing | Arkansas, US, United States | missing | آرکنساس | missing | 2D Polygon | 3.5 | missing | missing | Arkansas | missing | US | missing | Arkansas | missing | 0 | Arkansas | missing | Арканзас | missing | missing | USA | missing | missing | missing | Арканзас | 1 | State | 4099753 | 1 | 1159315355 | अरकांसास | missing |
| 16 | missing | missing | missing | http://en.wikipedia.org/wiki/Iowa | Iowa | missing | United States of America | missing | USA | Iowa | 아이오와 | Iowa | United States of America | US.IA | Iowa | missing | Iowa | missing | IA|Iowa | State | Q1546 | 1 | Iowa | missing | -1 | missing | -93.3891 | 1 | missing | Midwest | Iowa | -1 | West North Central | 2 | آيوا | 7.5 | 愛荷華州 | آیووا | missing | IA | 42.0423 | 20 | Iowa | missing | missing | missing | Iowa | -99 | US.IA | US19 | 2347574 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3529 | আইওয়া | איווה | Iowa | US19 | Άιοβα | Iowa | missing | 4 | missing | missing | アイオワ州 | 1 | missing | 3529 | missing | missing | 1 | 2 | missing | missing | 艾奥瓦州 | 0 | US-IA | missing | Iowa | Iowa | Iowa | missing | Iowa, US, United States | missing | آئیووا | missing | 2D Polygon | 3.5 | missing | missing | Iowa | missing | US | missing | Iowa | missing | 0 | Iowa | missing | Айова | missing | missing | USA | missing | missing | missing | Айова | 1 | State | 4862182 | 1 | 1159315357 | आयोवा | missing |
| 17 | missing | missing | missing | http://en.wikipedia.org/wiki/Kansas | Kansas | missing | United States of America | missing | USA | Kansas | 캔자스 | Kansas | United States of America | US.KS | Kansas | missing | Kansas | missing | KS|Kans. | State | Q1558 | 1 | Kansas | missing | -1 | missing | -98.3309 | 1 | missing | Midwest | Kansas | -1 | West North Central | 2 | كانساس | 7.5 | 堪薩斯州 | کانزاس | missing | KS | 38.5 | 20 | Kansas | missing | missing | missing | Kansas | -99 | US.KS | US20 | 2347575 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3530 | ক্যান্সাস | קנזס | Kansas | US20 | Κάνσας | Kansas | missing | 6 | missing | missing | カンザス州 | 1 | missing | 3530 | missing | missing | 1 | 2 | missing | missing | 堪萨斯州 | 0 | US-KS | missing | Kans. | Kansas | Kansas | missing | Kansas, US, United States | missing | کنساس | missing | 2D Polygon | 3.5 | missing | missing | Kansas | missing | US | missing | Kansas | missing | 0 | Kansas | missing | Канзас | missing | missing | USA | missing | missing | missing | Канзас | 1 | State | 4273857 | 1 | 1159315359 | केन्सास | missing |
| 18 | missing | missing | missing | http://en.wikipedia.org/wiki/Missouri | Missouri | missing | United States of America | missing | USA | Missouri | 미주리 | Missouri | United States of America | US.MO | Missouri | missing | Missouri | missing | MO | State | Q1581 | 1 | Missouri | missing | -1 | missing | -92.446 | 1 | missing | Midwest | Missouri | -1 | West North Central | 2 | ميزوري | 7.5 | 密蘇里州 | میزوری | missing | MO | 38.5487 | 20 | Missouri | missing | missing | missing | Missouri | -99 | US.MO | US29 | 2347584 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3531 | মিসৌরি | מיזורי | Missouri | US29 | Μιζούρι | Missouri | missing | 8 | US17 | missing | ミズーリ州 | 1 | missing | 3531 | missing | missing | 1 | 2 | missing | missing | 密苏里州 | 0 | US-MO | missing | Mo. | Missouri | Missouri | missing | Missouri, US, United States | missing | مسوری | missing | 2D Polygon | 3.5 | missing | missing | Missouri | missing | US | US.IL|USA-MOS | Misuri | missing | 0 | Missouri | missing | Миссури | missing | missing | USA | missing | missing | missing | Міссурі | 1 | State | 4398678 | 1 | 1159315361 | मिसौरी | missing |
| 19 | missing | missing | missing | http://en.wikipedia.org/wiki/Nebraska | Nebraska | missing | United States of America | missing | USA | Nebraska | 네브래스카 | Nebraska | United States of America | US.NE | Nebraska | missing | Nebraska | missing | NE|Nebr. | State | Q1553 | 1 | Nebraska | missing | -1 | missing | -99.6855 | 1 | missing | Midwest | Nebraska | -1 | West North Central | 2 | نبراسكا | 7.5 | 內布拉斯加州 | نبراسکا | missing | NE | 41.5002 | 20 | Nebraska | missing | missing | missing | Nebraska | -99 | US.NE | US31 | 2347586 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3532 | নেব্রাস্কা | נברסקה | Nebraska | US31 | Νεμπράσκα | Nebraska | missing | 8 | missing | missing | ネブラスカ州 | 1 | missing | 3532 | missing | missing | 1 | 2 | missing | missing | 內布拉斯加州 | 0 | US-NE | missing | Nebr. | Nebraska | Nebraska | missing | Nebraska, US, United States | missing | نیبراسکا | missing | 2D Polygon | 3.5 | missing | missing | Nebraska | missing | US | missing | Nebraska | missing | 0 | Nebraska | missing | Небраска | missing | missing | USA | missing | missing | missing | Небраска | 1 | State | 5073708 | 1 | 1159315363 | नेब्रास्का | missing |
| 20 | missing | missing | missing | http://en.wikipedia.org/wiki/Oklahoma | Oklahoma | missing | United States of America | missing | USA | Oklahoma | 오클라호마 | Oklahoma | United States of America | US.OK | Oklahoma | missing | Oklahoma | missing | OK|Okla. | State | Q1649 | 1 | Oklahoma | missing | -1 | missing | -97.1309 | 1 | missing | South | Oklahoma | -1 | West South Central | 2 | أوكلاهوما | 7.5 | 奧克拉荷馬州 | اکلاهما | missing | OK | 35.452 | 20 | Oklahoma | missing | missing | missing | Oklahoma | -99 | US.OK | US40 | 2347595 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3533 | ওকলাহোমা | אוקלהומה | Oklahoma | US40 | Οκλαχόμα | Oklahoma | missing | 8 | missing | missing | オクラホマ州 | 1 | missing | 3533 | missing | missing | 1 | 2 | missing | missing | 俄克拉荷马州 | 0 | US-OK | missing | Okla. | Oklahoma | Oklahoma | missing | Oklahoma, US, United States | missing | اوکلاہوما | missing | 2D Polygon | 3.5 | missing | missing | Oklahoma | missing | US | missing | Oklahoma | missing | 0 | Oklahoma | missing | Оклахома | missing | missing | USA | missing | missing | missing | Оклахома | 1 | State | 4544379 | 1 | 1159315365 | ओक्लाहोमा | missing |
| 21 | missing | missing | missing | http://en.wikipedia.org/wiki/South_Dakota | South Dakota | missing | United States of America | missing | USA | Güney Dakota | 사우스다코타 | South Dakota | United States of America | US.SD | South Dakota | missing | Dakota du Sud | missing | SD|S.D. | State | Q1211 | 1 | Dakota do Sul | missing | -1 | missing | -100.255 | 1 | missing | Midwest | South Dakota | -1 | West North Central | 2 | داكوتا الجنوبية | 7.5 | 南達科他州 | داکوتای جنوبی | missing | SD | 44.4711 | 20 | South Dakota | missing | missing | missing | Dél-Dakota | -99 | US.SD | US46 | 2347600 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3534 | দক্ষিণ ডাকোটা | דקוטה הדרומית | South Dakota | US46 | Νότια Ντακότα | South Dakota | missing | 12 | missing | missing | サウスダコタ州 | 1 | missing | 3534 | missing | missing | 1 | 2 | missing | missing | 南达科他州 | 0 | US-SD | missing | S.D. | Nam Dakota | Dakota del Sud | missing | South Dakota, US, United States | missing | جنوبی ڈکوٹا | missing | 2D Polygon | 3.5 | missing | missing | Dakota Południowa | missing | US | missing | Dakota del Sur | missing | 0 | Dakota Selatan | missing | Южная Дакота | missing | missing | USA | missing | missing | missing | Південна Дакота | 1 | State | 5769223 | 1 | 1159315367 | दक्षिण डकोटा | missing |
| 22 | missing | missing | missing | http://en.wikipedia.org/wiki/Louisiana | Louisiana | missing | United States of America | missing | USA | Louisiana | 루이지애나 | Louisiana | United States of America | US.LA | Louisiana | missing | Louisiane | missing | LA | State | Q1588 | 5 | Luisiana | missing | -1 | missing | -91.9991 | 1 | missing | South | Louisiana | -1 | West South Central | 2 | لويزيانا | 7.5 | 路易斯安那州 | لوئیزیانا | missing | LA | 30.5274 | 20 | Louisiana | missing | missing | missing | Louisiana | -99 | US.LA | US22 | 2347577 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3535 | লুইজিয়ানা | לואיזיאנה | Louisiana | US22 | Λουιζιάνα | Louisiana | missing | 9 | missing | missing | ルイジアナ州 | 1 | missing | 3535 | missing | missing | 1 | 2 | missing | missing | 路易斯安那州 | 0 | US-LA | missing | La. | Louisiana | Louisiana | missing | Louisiana, US, United States | missing | لوزیانا | missing | 2D Polygon | 3.5 | missing | missing | Luizjana | missing | US | missing | Luisiana | missing | 0 | Louisiana | missing | Луизиана | missing | missing | USA | missing | missing | missing | Луїзіана | 1 | State | 4331987 | 1 | 1159315221 | लुईज़ियाना | missing |
| 23 | missing | missing | missing | http://en.wikipedia.org/wiki/Texas | Texas | missing | United States of America | missing | USA | Teksas | 텍사스 | Texas | United States of America | US.TX | Texas | missing | Texas | missing | TX|Tex. | State | Q1439 | 4 | Texas | missing | -1 | missing | -98.7607 | 1 | missing | South | Texas | -1 | West South Central | 2 | تكساس | 7.5 | 德克薩斯州 | تگزاس | missing | TX | 31.131 | 20 | Texas | missing | missing | missing | Texas | -99 | US.TX | US48 | 2347602 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3536 | টেক্সাস | טקסס | Texas | US48 | Τέξας | Texas | missing | 5 | missing | missing | テキサス州 | 1 | missing | 3536 | missing | missing | 1 | 2 | missing | missing | 得克萨斯州 | 0 | US-TX | missing | Tex. | Texas | Texas | missing | Texas, US, United States | missing | ٹیکساس | missing | 2D Polygon | 3.5 | missing | missing | Teksas | missing | US | missing | Texas | missing | 0 | Texas | missing | Техас | missing | missing | USA | missing | missing | missing | Техас | 1 | State | 4736286 | 1 | 1159315211 | टॅक्सस | missing |
| 24 | missing | missing | missing | http://en.wikipedia.org/wiki/Connecticut | Connecticut | missing | United States of America | missing | USA | Connecticut | 코네티컷 | Connecticut | United States of America | US.CT | Connecticut | missing | Connecticut | missing | CT|Conn. | State | Q779 | 1 | Connecticut | missing | -1 | missing | -72.7594 | 1 | missing | Northeast | Connecticut | -1 | New England | 2 | كونيتيكت | 7.5 | 康乃狄克州 | کانتیکت | missing | CT | 41.6486 | 20 | Connecticut | missing | missing | missing | Connecticut | -99 | US.CT | US09 | 2347565 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3537 | কানেটিকাট | קונטיקט | Connecticut | US09 | Κονέκτικατ | Connecticut | missing | 11 | missing | missing | コネチカット州 | 1 | missing | 3537 | missing | missing | 1 | 2 | missing | missing | 康涅狄格州 | 0 | US-CT | missing | Conn. | Connecticut | Connecticut | missing | Connecticut, US, United States | missing | کنیکٹیکٹ | missing | 2D Polygon | 3.5 | missing | missing | Connecticut | missing | US | missing | Connecticut | missing | 0 | Connecticut | missing | Коннектикут | missing | missing | USA | missing | missing | missing | Коннектикут | 1 | State | 4831725 | 1 | 1159315301 | कनेक्टिकट | missing |
| 25 | missing | missing | missing | http://en.wikipedia.org/wiki/Massachusetts | Massachusetts | missing | United States of America | missing | USA | Massachusetts | 매사추세츠 | Massachusetts | United States of America | US.MA | Massachusetts | missing | Massachusetts | missing | Commonwealth of Massachusetts|MA|Mass. | State | Q771 | 6 | Massachusetts | missing | -1 | missing | -71.9993 | 1 | missing | Northeast | Massachusetts | -1 | New England | 2 | ماساتشوستس | 7.5 | 麻薩諸塞州 | ماساچوست | missing | MA | 42.3739 | 20 | Massachusetts | missing | missing | missing | Massachusetts | -99 | US.MA | US25 | 2347580 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3513 | ম্যাসাচুসেটস | מסצ'וסטס | Massachusetts | US25 | Μασαχουσέτη | Massachusetts | missing | 13 | missing | missing | マサチューセッツ州 | 1 | missing | 3513 | missing | missing | 1 | 2 | missing | missing | 马萨诸塞州 | 0 | US-MA | missing | Mass. | Massachusetts | Massachusetts | missing | Massachusetts, US, United States | missing | میساچوسٹس | missing | 2D Polygon | 3.5 | missing | missing | Massachusetts | missing | US | missing | Massachusetts | missing | 0 | Massachusetts | missing | Массачусетс | missing | missing | USA | missing | missing | missing | Массачусетс | 1 | State | 6254926 | 1 | 1159312157 | मैसाचूसिट्स | missing |
| 26 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Hampshire | New Hampshire | missing | United States of America | missing | USA | New Hampshire | 뉴햄프셔 | New Hampshire | United States of America | US.NH | New Hampshire | missing | New Hampshire | missing | NH|N.H. | State | Q759 | 1 | Nova Hampshire | missing | -1 | missing | -71.6301 | 1 | missing | Northeast | New Hampshire | -1 | New England | 2 | نيوهامبشير | 7.5 | 新罕布夏州 | نیوهمپشایر | missing | NH | 43.5993 | 20 | New Hampshire | missing | missing | missing | New Hampshire | -99 | US.NH | US33 | 2347588 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3538 | নিউ হ্যাম্প্শায়ার | ניו המפשייר | New Hampshire | US33 | Νιου Χάμσαϊρ | New Hampshire | missing | 13 | missing | missing | ニューハンプシャー州 | 1 | missing | 3538 | missing | missing | 1 | 2 | missing | missing | 新罕布什尔州 | 0 | US-NH | missing | N.H. | New Hampshire | New Hampshire | missing | New Hampshire, US, United States | missing | نیو ہیمپشائر | missing | 2D Polygon | 3.5 | missing | missing | New Hampshire | missing | US | missing | Nuevo Hampshire | missing | 0 | New Hampshire | missing | Нью-Гэмпшир | missing | missing | USA | missing | missing | missing | Нью-Гемпшир | 1 | State | 5090174 | 1 | 1159315303 | नया हेम्पशायर | missing |
| 27 | missing | missing | missing | http://en.wikipedia.org/wiki/Rhode_Island | Rhode Island | missing | United States of America | missing | USA | Rhode Island | 로드아일랜드 | Rhode Island | United States of America | US.RI | Rhode Island | missing | Rhode Island | missing | State of Rhode Island and Providence Plantations|RI|R.I. | State | Q1387 | 6 | Rhode Island | missing | -1 | missing | -71.5082 | 1 | missing | Northeast | Rhode Island | -1 | New England | 2 | رود آيلاند | 7.5 | 羅德島州 | رود آیلند | missing | RI | 41.6242 | 20 | Rhode Island | missing | missing | missing | Rhode Island | -99 | US.RI | US44 | 2347598 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3539 | রোড আইল্যান্ড | רוד איילנד | Rhode Island | US44 | Ρόουντ Άιλαντ | Rhode Island | missing | 12 | missing | missing | ロードアイランド州 | 1 | missing | 3539 | missing | missing | 1 | 2 | missing | missing | 罗得岛州 | 0 | US-RI | missing | R.I. | Rhode Island | Rhode Island | missing | Rhode Island, US, United States | missing | رہوڈ آئی لینڈ | missing | 2D Polygon | 3.5 | missing | missing | Rhode Island | missing | US | missing | Rhode Island | missing | 0 | Rhode Island | missing | Род-Айленд | missing | missing | USA | missing | missing | missing | Род-Айленд | 1 | State | 5224323 | 1 | 1159312213 | रोड आइलैंड | missing |
| 28 | missing | missing | missing | http://en.wikipedia.org/wiki/Vermont | Vermont | missing | United States of America | missing | USA | Vermont | 버몬트 | Vermont | United States of America | US.VT | Vermont | missing | Vermont | missing | VT | State | Q16551 | 1 | Vermont | missing | -1 | missing | -72.7317 | 1 | missing | Northeast | Vermont | -1 | New England | 2 | فيرمونت | 7.5 | 佛蒙特州 | ورمونت | missing | VT | 44.0886 | 20 | Vermont | missing | missing | missing | Vermont | -99 | US.VT | US50 | 2347604 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3540 | ভার্মন্ট | ורמונט | Vermont | US50 | Βερμόντ | Vermont | missing | 7 | missing | missing | バーモント州 | 1 | missing | 3540 | missing | missing | 1 | 2 | missing | missing | 佛蒙特州 | 0 | US-VT | missing | Vt. | Vermont | Vermont | missing | Vermont, US, United States | missing | ورمونٹ | missing | 2D Polygon | 3.5 | missing | missing | Vermont | missing | US | missing | Vermont | missing | 0 | Vermont | missing | Вермонт | missing | missing | USA | missing | missing | missing | Вермонт | 1 | State | 5242283 | 1 | 1159315305 | वर्मांट | missing |
| 29 | missing | missing | missing | http://en.wikipedia.org/wiki/Alabama | Alabama | missing | United States of America | missing | USA | Alabama | 앨라배마 | Alabama | United States of America | US.AL | Alabama | missing | Alabama | missing | AL|Ala. | State | Q173 | 5 | Alabama | missing | -1 | missing | -86.7184 | 1 | missing | South | Alabama | -1 | East South Central | 2 | ألاباما | 7.5 | 阿拉巴馬州 | آلاباما | missing | AL | 32.8551 | 20 | Alabama | missing | missing | missing | Alabama | -99 | US.AL | US01 | 2347559 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3541 | অ্যালাবামা | אלבמה | Alabama | US01 | Αλαμπάμα | Alabama | missing | 7 | missing | missing | アラバマ州 | 1 | missing | 3541 | missing | missing | 1 | 2 | missing | missing | 亚拉巴马州 | 0 | US-AL | missing | Ala. | Alabama | Alabama | missing | Alabama, US, United States | missing | الاباما | missing | 2D Polygon | 3.5 | missing | missing | Alabama | missing | US | missing | Alabama | missing | 0 | Alabama | missing | Алабама | missing | missing | USA | missing | missing | missing | Алабама | 1 | State | 4829764 | 1 | 1159315233 | अलाबामा | missing |
| 30 | missing | missing | missing | http://en.wikipedia.org/wiki/Florida | Florida | missing | United States of America | missing | USA | Florida | 플로리다 | Florida | United States of America | US.FL | Florida | missing | Floride | missing | FL|Fla. | State | Q812 | 5 | Flórida | missing | -1 | missing | -81.6228 | 1 | missing | South | Florida | -1 | South Atlantic | 2 | فلوريدا | 7.5 | 佛羅里達州 | فلوریدا | missing | FL | 28.1568 | 20 | Florida | missing | missing | missing | Florida | -99 | US.FL | US12 | 2347568 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3542 | ফ্লোরিডা | פלורידה | Florida | US12 | Φλόριντα | Florida | missing | 7 | missing | missing | フロリダ州 | 8 | missing | 3542 | missing | missing | 1 | 2 | missing | missing | 佛罗里达州 | 0 | US-FL | missing | Fla. | Florida | Florida | missing | Florida, US, United States | missing | فلوریڈا | missing | 2D Polygon | 3.5 | missing | missing | Floryda | missing | US | missing | Florida | missing | 0 | Florida | missing | Флорида | missing | missing | USA | missing | missing | missing | Флорида | 1 | State | 4155751 | 1 | 1159315207 | फ़्लोरिडा | missing |
| 31 | missing | missing | missing | http://en.wikipedia.org/wiki/Georgia_(U.S._state) | Georgia | missing | United States of America | missing | USA | Georgia | 조지아 | Georgia | United States of America | US.GA | Georgia | missing | Géorgie | missing | GA|Ga. | State | Q1428 | 6 | Geórgia | missing | -1 | missing | -83.4078 | 1 | missing | South | Georgia | -1 | South Atlantic | 2 | جورجيا | 7.5 | 喬治亞州 | جورجیا | missing | GA | 32.8547 | 20 | Georgia | missing | missing | missing | Georgia | -99 | US.GA | US13 | 2347569 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3543 | জর্জিয়া | ג'ורג'יה | Georgia | US13 | Τζόρτζια | Georgia | missing | 7 | missing | missing | ジョージア州 | 1 | missing | 3543 | missing | missing | 1 | 2 | missing | missing | 佐治亚州 | 0 | US-GA | missing | Ga. | Georgia | Georgia | missing | Georgia, US, United States | missing | ریاست جارجیا | missing | 2D Polygon | 3.5 | missing | missing | Georgia | missing | US | missing | Georgia | missing | 0 | Georgia | missing | Джорджия | missing | missing | USA | missing | missing | missing | Джорджія | 1 | State | 4197000 | 1 | 1159311857 | जॉर्जिया | missing |
| 32 | missing | missing | missing | http://en.wikipedia.org/wiki/Mississippi | Mississippi | missing | United States of America | missing | USA | Mississippi | 미시시피 | Mississippi | United States of America | US.MS | Mississippi | missing | Mississippi | missing | MS|Miss. | State | Q1494 | 5 | Mississippi | missing | -1 | missing | -89.7189 | 1 | missing | South | Mississippi | -1 | East South Central | 2 | مسيسيبي | 7.5 | 密西西比州 | میسیسیپی | missing | MS | 32.8657 | 20 | Mississippi | missing | missing | missing | Mississippi | -99 | US.MS | US28 | 2347583 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3544 | মিসিসিপি | מיסיסיפי | Mississippi | US28 | Μισισίπι | Mississippi | missing | 11 | missing | missing | ミシシッピ州 | 1 | missing | 3544 | missing | missing | 1 | 2 | missing | missing | 密西西比州 | 0 | US-MS | missing | Miss. | Mississippi | Mississippi | missing | Mississippi, US, United States | missing | مسیسپی | missing | 2D Polygon | 3.5 | missing | missing | Missisipi | missing | US | missing | Misisipi | missing | 0 | Mississippi | missing | Миссисипи | missing | missing | USA | missing | missing | missing | Міссісіпі | 1 | State | 4436296 | 1 | 1159315231 | मिसिसिप्पी | missing |
| 33 | missing | missing | missing | http://en.wikipedia.org/wiki/South_Carolina | South Carolina | missing | United States of America | missing | USA | Güney Karolina | 사우스캐롤라이나 | South Carolina | United States of America | US.SC | South Carolina | missing | Caroline du Sud | missing | SC|S.C. | State | Q1456 | 1 | Carolina do Sul | missing | -1 | missing | -80.6471 | 1 | missing | South | South Carolina | -1 | South Atlantic | 2 | كارولاينا الجنوبية | 7.5 | 南卡羅萊納州 | کارولینای جنوبی | missing | SC | 33.8578 | 20 | South Carolina | missing | missing | missing | Dél-Karolina | -99 | US.SC | US45 | 2347599 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3545 | সাউথ ক্যারোলাইনা | קרוליינה הדרומית | South Carolina | US45 | Νότια Καρολίνα | South Carolina | missing | 14 | missing | missing | サウスカロライナ州 | 1 | missing | 3545 | missing | missing | 1 | 2 | missing | missing | 南卡罗来纳州 | 0 | US-SC | missing | S.C. | Nam Carolina | Carolina del Sud | missing | South Carolina, US, United States | missing | جنوبی کیرولینا | missing | 2D Polygon | 3.5 | missing | missing | Karolina Południowa | missing | US | missing | Carolina del Sur | missing | 0 | Carolina Selatan | missing | Южная Каролина | missing | missing | USA | missing | missing | missing | Південна Кароліна | 1 | State | 4597040 | 1 | 1159315307 | दक्षिणी केरोलाइना | missing |
| 34 | missing | missing | missing | http://en.wikipedia.org/wiki/Illinois | Illinois | missing | United States of America | missing | USA | Illinois | 일리노이 | Illinois | United States of America | US.IL | Illinois | missing | Illinois | missing | IL|Ill. | State | Q1204 | 1 | Illinois | missing | -1 | missing | -89.1991 | 1 | missing | Midwest | Illinois | -1 | East North Central | 2 | إلينوي | 7.5 | 伊利諾州 | ایلینوی | missing | IL | 39.946 | 20 | Illinois | missing | missing | missing | Illinois | -99 | US.IL | US17 | 2347572 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3546 | ইলিনয় | אילינוי | Illinois | US17 | Ιλινόι | Illinois | missing | 8 | missing | missing | イリノイ州 | 1 | missing | 3546 | missing | missing | 1 | 2 | missing | missing | 伊利诺伊州 | 0 | US-IL | missing | Ill. | Illinois | Illinois | missing | Illinois, US, United States | missing | الینوائے | missing | 2D Polygon | 3.5 | missing | missing | Illinois | missing | US | missing | Illinois | missing | 0 | Illinois | missing | Иллинойс | missing | missing | USA | missing | missing | missing | Іллінойс | 1 | State | 4896861 | 1 | 1159315309 | इलिनॉय | missing |
| 35 | missing | missing | missing | http://en.wikipedia.org/wiki/Indiana | Indiana | missing | United States of America | missing | USA | Indiana | 인디애나 | Indiana | United States of America | US.IN | Indiana | missing | Indiana | missing | IN|Ind. | State | Q1415 | 1 | Indiana | missing | -1 | missing | -86.1396 | 1 | missing | Midwest | Indiana | -1 | East North Central | 2 | إنديانا | 7.5 | 印第安纳州 | ایندیانا | missing | IN | 39.8874 | 20 | Indiana | missing | missing | missing | Indiana | -99 | US.IN | US18 | 2347573 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3547 | ইন্ডিয়ানা | אינדיאנה | Indiana | US18 | Ιντιάνα | Indiana | missing | 7 | missing | missing | インディアナ州 | 1 | missing | 3547 | missing | missing | 1 | 2 | missing | missing | 印第安纳州 | 0 | US-IN | missing | Ind. | Indiana | Indiana | missing | Indiana, US, United States | missing | انڈیانا | missing | 2D Polygon | 3.5 | missing | missing | Indiana | missing | US | missing | Indiana | missing | 0 | Indiana | missing | Индиана | missing | missing | USA | missing | missing | missing | Індіана | 1 | State | 4921868 | 1 | 1159315311 | इंडियाना | missing |
| 36 | missing | missing | missing | http://en.wikipedia.org/wiki/Kentucky | Kentucky | missing | United States of America | missing | USA | Kentucky | 켄터키 | Kentucky | United States of America | US.KY | Kentucky | missing | Kentucky | missing | Commonwealth of Kentucky|KY | State | Q1603 | 1 | Kentucky | missing | -1 | missing | -85.5729 | 1 | missing | South | Kentucky | -1 | East South Central | 2 | كنتاكي | 7.5 | 肯塔基州 | کنتاکی | missing | KY | 37.3994 | 20 | Kentucky | missing | missing | missing | Kentucky | -99 | US.KY | US21 | 2347576 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3548 | কেন্টাকি | קנטקי | Kentucky | US21 | Κεντάκι | Kentucky | missing | 8 | US18 | missing | ケンタッキー州 | 1 | missing | 3548 | missing | missing | 1 | 2 | missing | missing | 肯塔基州 | 0 | US-KY | missing | Ky. | Kentucky | Kentucky | missing | Kentucky, US, United States | missing | کینٹکی | missing | 2D Polygon | 3.5 | missing | missing | Kentucky | missing | US | US.IN|USA-KEN | Kentucky | missing | 0 | Kentucky | missing | Кентукки | missing | missing | USA | missing | missing | missing | Кентуккі | 1 | State | 6254925 | 1 | 1159315313 | केन्टकी | missing |
| 37 | missing | missing | missing | http://en.wikipedia.org/wiki/North_Carolina | North Carolina | missing | United States of America | missing | USA | Kuzey Karolina | 노스캐롤라이나 | North Carolina | United States of America | US.NC | North Carolina | missing | Caroline du Nord | missing | NC|N.C. | State | Q1454 | 5 | Carolina do Norte | missing | -1 | missing | -78.866 | 1 | missing | South | North Carolina | -1 | South Atlantic | 2 | كارولاينا الشمالية | 7.5 | 北卡羅萊納州 | کارولینای شمالی | missing | NC | 35.6152 | 20 | North Carolina | missing | missing | missing | Észak-Karolina | -99 | US.NC | US37 | 2347592 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3549 | নর্থ ক্যারোলাইনা | קרוליינה הצפונית | North Carolina | US37 | Βόρεια Καρολίνα | North Carolina | missing | 14 | missing | missing | ノースカロライナ州 | 1 | missing | 3549 | missing | missing | 1 | 2 | missing | missing | 北卡罗来纳州 | 0 | US-NC | missing | N.C. | Bắc Carolina | Carolina del Nord | missing | North Carolina, US, United States | missing | شمالی کیرولینا | missing | 2D Polygon | 3.5 | missing | missing | Karolina Północna | missing | US | missing | Carolina del Norte | missing | 0 | Carolina Utara | missing | Северная Каролина | missing | missing | USA | missing | missing | missing | Північна Кароліна | 1 | State | 4482348 | 1 | 1159314887 | उत्तरी केरोलिना | missing |
| 38 | missing | missing | missing | http://en.wikipedia.org/wiki/Ohio | Ohio | missing | United States of America | missing | USA | Ohio | 오하이오 | Ohio | United States of America | US.OH | Ohio | missing | Ohio | missing | OH|Ohio | State | Q1397 | 1 | Ohio | missing | -1 | missing | -82.6719 | 1 | missing | Midwest | Ohio | -1 | East North Central | 2 | أوهايو | 7.5 | 俄亥俄州 | اوهایو | missing | OH | 40.0924 | 20 | Ohio | missing | missing | missing | Ohio | -99 | US.OH | US39 | 2347594 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3550 | ওহাইও | אוהיו | Ohio | US39 | Οχάιο | Ohio | missing | 4 | missing | missing | オハイオ州 | 1 | missing | 3550 | missing | missing | 1 | 2 | missing | missing | 俄亥俄州 | 0 | US-OH | missing | Ohio | Ohio | Ohio | missing | Ohio, US, United States | missing | اوہائیو | missing | 2D Polygon | 3.5 | missing | missing | Ohio | missing | US | missing | Ohio | missing | 0 | Ohio | missing | Огайо | missing | missing | USA | missing | missing | missing | Огайо | 1 | State | 5165418 | 1 | 1159315315 | ओहायो | missing |
| 39 | missing | missing | missing | http://en.wikipedia.org/wiki/Tennessee | Tennessee | missing | United States of America | missing | USA | Tennessee | 테네시 | Tennessee | United States of America | US.TN | Tennessee | missing | Tennessee | missing | TN|Tenn. | State | Q1509 | 1 | Tennessee | missing | -1 | missing | -86.3415 | 1 | missing | South | Tennessee | -1 | East South Central | 2 | تينيسي | 7.5 | 田納西州 | تنسی | missing | TN | 35.7514 | 20 | Tennessee | missing | missing | missing | Tennessee | -99 | US.TN | US47 | 2347601 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3551 | টেনেসী | טנסי | Tennessee | US47 | Τενεσί | Tennessee | missing | 9 | missing | missing | テネシー州 | 1 | missing | 3551 | missing | missing | 1 | 2 | missing | missing | 田纳西州 | 0 | US-TN | missing | Tenn. | Tennessee | Tennessee | missing | Tennessee, US, United States | missing | ٹینیسی | missing | 2D Polygon | 3.5 | missing | missing | Tennessee | missing | US | missing | Tennessee | missing | 0 | Tennessee | missing | Теннесси | missing | missing | USA | missing | missing | missing | Теннессі | 1 | State | 4662168 | 1 | 1159315319 | टेनेसी | missing |
| 40 | missing | missing | missing | http://en.wikipedia.org/wiki/Virginia | Virginia | missing | United States of America | missing | USA | Virjinya | 버지니아 | Virginia | United States of America | US.VA | Virginia | missing | Virginie | missing | VA | State | Q1370 | 6 | Virgínia | missing | -1 | missing | -78.2431 | 1 | missing | South | Virginia | -1 | South Atlantic | 2 | فرجينيا | 7.5 | 維吉尼亞州 | ویرجینیا | missing | VA | 37.7403 | 20 | Virginia | missing | missing | missing | Virginia | -99 | US.VA | US51 | 2347605 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3552 | ভার্জিনিয়া | וירג'יניה | Virginia | US51 | Βιρτζίνια | Virginia | missing | 8 | missing | missing | バージニア州 | 1 | missing | 3552 | missing | missing | 1 | 2 | missing | missing | 弗吉尼亚州 | 0 | US-VA | missing | Va. | Virginia | Virginia | missing | Virginia, US, United States | missing | ورجینیا | missing | 2D MultiPolygon | 3.5 | missing | missing | Wirginia | missing | US | missing | Virginia | missing | 0 | Virginia | missing | Виргиния | missing | missing | USA | missing | missing | missing | Вірджинія | 1 | State | 6254928 | 1 | 1159315259 | वर्जीनिया | missing |
| 41 | missing | missing | missing | http://en.wikipedia.org/wiki/Wisconsin | Wisconsin | missing | United States of America | missing | USA | Wisconsin | 위스콘신 | Wisconsin | United States of America | US.WI | Wisconsin | missing | Wisconsin | missing | WI|Wis. | State | Q1537 | 1 | Wisconsin | missing | -1 | missing | -89.5831 | 1 | missing | Midwest | Wisconsin | -1 | East North Central | 2 | ويسكونسن | 7.5 | 威斯康辛州 | ویسکانسین | missing | WI | 44.3709 | 20 | Wisconsin | missing | missing | missing | Wisconsin | -99 | US.WI | US55 | 2347608 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3553 | উইসকনসিন | ויסקונסין | Wisconsin | US55 | Ουισκόνσιν | Wisconsin | missing | 9 | missing | missing | ウィスコンシン州 | 1 | missing | 3553 | missing | missing | 1 | 2 | missing | missing | 威斯康星州 | 0 | US-WI | missing | Wis. | Wisconsin | Wisconsin | missing | Wisconsin, US, United States | missing | وسکونسن | missing | 2D Polygon | 3.5 | missing | missing | Wisconsin | missing | US | missing | Wisconsin | missing | 0 | Wisconsin | missing | Висконсин | missing | missing | USA | missing | missing | missing | Вісконсин | 1 | State | 5279468 | 1 | 1159315321 | विस्कॉन्सिन | missing |
| 42 | missing | missing | missing | http://en.wikipedia.org/wiki/West_Virginia | West Virginia | missing | United States of America | missing | USA | Batı Virginia | 웨스트버지니아 | West Virginia | United States of America | US.WV | West Virginia | missing | Virginie-Occidentale | missing | WV|W.Va. | State | Q1371 | 1 | Virgínia Ocidental | missing | -1 | missing | -80.7128 | 1 | missing | South | West Virginia | -1 | South Atlantic | 2 | فيرجينيا الغربية | 7.5 | 西維吉尼亞州 | ویرجینیای غربی | missing | WV | 38.6422 | 20 | West Virginia | missing | missing | missing | Nyugat-Virginia | -99 | US.WV | US54 | 2347607 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3554 | পশ্চিম ভার্জিনিয়া | וירג'יניה המערבית | West Virginia | US54 | Δυτική Βιρτζίνια | West Virginia | missing | 13 | missing | missing | ウェストバージニア州 | 1 | missing | 3554 | missing | missing | 1 | 2 | missing | missing | 西維吉尼亞州 | 0 | US-WV | missing | W.Va. | Tây Virginia | Virginia Occidentale | missing | West Virginia, US, United States | missing | مغربی ورجینیا | missing | 2D Polygon | 3.5 | missing | missing | Wirginia Zachodnia | missing | US | missing | Virginia Occidental | missing | 0 | Virginia Barat | missing | Западная Виргиния | missing | missing | USA | missing | missing | missing | Західна Вірджинія | 1 | State | 4826850 | 1 | 1159315323 | पश्चिमी वर्जीनिया | missing |
| 43 | missing | missing | missing | http://en.wikipedia.org/wiki/Delaware | Delaware | missing | United States of America | missing | USA | Delaware | 델라웨어 | Delaware | United States of America | US.DE | Delaware | missing | Delaware | missing | DE|Del. | State | Q1393 | 1 | Delaware | missing | -1 | missing | -75.4112 | 1 | missing | South | Delaware | -1 | South Atlantic | 2 | ديلاوير | 7.5 | 特拉華州 | دلاویر | missing | DE | 38.8657 | 20 | Delaware | missing | missing | missing | Delaware | -99 | US.DE | US10 | 2347566 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3555 | ডেলাওয়্যার | דלאוור | Delaware | US10 | Ντέλαγουερ | Delaware | missing | 8 | missing | missing | デラウェア州 | 1 | missing | 3555 | missing | missing | 1 | 2 | missing | missing | 特拉华州 | 0 | US-DE | missing | Del. | Delaware | Delaware | missing | Delaware, US, United States | missing | ڈیلاویئر | missing | 2D Polygon | 3.5 | missing | missing | Delaware | missing | US | missing | Delaware | missing | 0 | Delaware | missing | Делавэр | missing | missing | USA | missing | missing | missing | Делавер | 1 | State | 4142224 | 1 | 1159315325 | डेलावेयर | missing |
| 44 | missing | missing | missing | http://en.wikipedia.org/wiki/Washington,_D.C. | Washington | missing | United States of America | missing | USA | Washington | 워싱턴 D.C. | District of Columbia | United States of America | US.DC | Washington D.C. | missing | Washington | missing | DC|D.C. | Federal District | Q61 | 1 | Washington | missing | -1 | missing | -77.0113 | 1 | missing | South | District of Columbia | -1 | South Atlantic | 2 | واشنطن | 7.5 | 華盛頓哥倫比亞特區 | واشینگتن، دی. سی. | missing | DC | 38.8922 | 20 | Washington | missing | missing | missing | Washington | 9 | US.DC | US11 | 2347567 | missing | missing | 9 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3556 | ওয়াশিংটন | וושינגטון די. סי. | Washington | US11 | Ουάσινγκτον | District of Columbia | missing | 20 | missing | missing | ワシントンD.C. | 1 | missing | 3556 | missing | missing | 1 | 2 | missing | missing | 华盛顿哥伦比亚特区 | 0 | US-DC | missing | D.C. | Washington | Washington | missing | District of Columbia, US, United States | missing | واشنگٹن ڈی سی | missing | 2D Polygon | 3.5 | missing | missing | Waszyngton | missing | US | missing | Washington D. C. | missing | 0 | Washington | missing | Вашингтон | missing | missing | USA | missing | missing | missing | Вашингтон | 1 | Federal District | 4138106 | 1 | 1159315327 | वॉशिंगटन डी॰ सी॰ | missing |
| 45 | missing | missing | missing | http://en.wikipedia.org/wiki/Maryland | Maryland | missing | United States of America | missing | USA | Maryland | 메릴랜드 | Maryland | United States of America | US.MD | Maryland | missing | Maryland | missing | MD | State | Q1391 | 1 | Maryland | missing | -1 | missing | -77.0454 | 1 | missing | South | Maryland | -1 | South Atlantic | 2 | ماريلند | 7.5 | 馬里蘭州 | مریلند | missing | MD | 39.3874 | 20 | Maryland | missing | missing | missing | Maryland | -99 | US.MD | US24 | 2347579 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3557 | মেরিল্যান্ড | מרילנד | Maryland | US24 | Μέριλαντ | Maryland | missing | 8 | missing | missing | メリーランド州 | 1 | missing | 3557 | missing | missing | 1 | 2 | missing | missing | 马里兰州 | 0 | US-MD | missing | Md. | Maryland | Maryland | missing | Maryland, US, United States | missing | میری لینڈ | missing | 2D Polygon | 3.5 | missing | missing | Maryland | missing | US | missing | Maryland | missing | 0 | Maryland | missing | Мэриленд | missing | missing | USA | missing | missing | missing | Меріленд | 1 | State | 4361885 | 1 | 1159315329 | मैरीलैंड | missing |
| 46 | missing | missing | missing | http://en.wikipedia.org/wiki/New_Jersey | New Jersey | missing | United States of America | missing | USA | New Jersey | 뉴저지 | New Jersey | United States of America | US.NJ | New Jersey | missing | New Jersey | missing | NJ|N.J. | State | Q1408 | 5 | Nova Jérsia | missing | -1 | missing | -74.4653 | 1 | missing | Northeast | New Jersey | -1 | Middle Atlantic | 2 | نيوجيرسي | 7.5 | 紐澤西州 | نیوجرسی | missing | NJ | 40.0449 | 20 | New Jersey | missing | missing | missing | New Jersey | -99 | US.NJ | US34 | 2347589 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3558 | নিউ জার্সি | ניו ג'רזי | New Jersey | US34 | Νιου Τζέρσεϊ | New Jersey | missing | 10 | missing | missing | ニュージャージー州 | 1 | missing | 3558 | missing | missing | 1 | 2 | missing | missing | 新泽西州 | 0 | US-NJ | missing | N.J. | New Jersey | New Jersey | missing | New Jersey, US, United States | missing | نیو جرسی | missing | 2D Polygon | 3.5 | missing | missing | New Jersey | missing | US | missing | Nueva Jersey | missing | 0 | New Jersey | missing | Нью-Джерси | missing | missing | USA | missing | missing | missing | Нью-Джерсі | 1 | State | 5101760 | 1 | 1159315267 | न्यू जर्सी | missing |
| 47 | missing | missing | missing | http://en.wikipedia.org/wiki/New_York | New York | missing | United States of America | missing | USA | New York | 뉴욕 | New York | United States of America | US.NY | New York | missing | État de New York | missing | NY|N.Y. | State | Q1384 | 3 | Nova Iorque | missing | -1 | missing | -75.3242 | 1 | missing | Northeast | New York | -1 | Middle Atlantic | 2 | نيويورك | 7.5 | 紐約州 | نیویورک | missing | NY | 43.1988 | 20 | New York | missing | missing | missing | New York | -99 | US.NY | US36 | 2347591 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3559 | নিউ ইয়র্ক | ניו יורק | New York | US36 | Νέα Υόρκη | New York | missing | 8 | missing | missing | ニューヨーク州 | 1 | missing | 3559 | missing | missing | 1 | 2 | missing | missing | 纽约州 | 0 | US-NY | missing | N.Y. | New York | New York | missing | New York, US, United States | missing | نیویارک | missing | 2D Polygon | 3.5 | missing | missing | Nowy Jork | missing | US | missing | Nueva York | missing | 0 | New York | missing | Нью-Йорк | missing | missing | USA | missing | missing | missing | штат Нью-Йорк | 1 | State | 5128638 | 1 | 1159312155 | न्यूयॉर्क | missing |
| 48 | missing | missing | missing | http://en.wikipedia.org/wiki/Pennsylvania | Pennsylvania | missing | United States of America | missing | USA | Pensilvanya | 펜실베이니아 | Pennsylvania | United States of America | US.PA | Pennsylvania | missing | Pennsylvanie | missing | Commonwealth of Pennsylvania|PA | State | Q1400 | 1 | Pensilvânia | missing | -1 | missing | -77.6094 | 1 | missing | Northeast | Pennsylvania | -1 | Middle Atlantic | 2 | بنسيلفانيا | 7.5 | 賓夕法尼亞州 | پنسیلوانیا | missing | PA | 40.8601 | 20 | Pennsylvania | missing | missing | missing | Pennsylvania | -99 | US.PA | US42 | 2347597 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3560 | পেনসিলভেনিয়া | פנסילבניה | Pennsylvania | US42 | Πενσιλβάνια | Pennsylvania | missing | 12 | missing | missing | ペンシルベニア州 | 1 | missing | 3560 | missing | missing | 1 | 2 | missing | missing | 宾夕法尼亚州 | 0 | US-PA | missing | Pa. | Pennsylvania | Pennsylvania | missing | Pennsylvania, US, United States | missing | پنسلوانیا | missing | 2D Polygon | 3.5 | missing | missing | Pensylwania | missing | US | missing | Pensilvania | missing | 0 | Pennsylvania | missing | Пенсильвания | missing | missing | USA | missing | missing | missing | Пенсильванія | 1 | State | 6254927 | 1 | 1159315331 | पेन्सिलवेनिया | missing |
| 49 | missing | missing | missing | http://en.wikipedia.org/wiki/Maine | Maine | missing | United States of America | missing | USA | Maine | 메인 | Maine | United States of America | US.ME | Maine | missing | Maine | missing | ME|Maine | State | Q724 | 6 | Maine | missing | -1 | missing | -69.1973 | 1 | missing | Northeast | Maine | -1 | New England | 2 | مين | 7.5 | 缅因州 | مین | missing | ME | 45.148 | 20 | Maine | missing | missing | missing | Maine | -99 | US.ME | US23 | 2347578 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3561 | মেইন | מיין | Maine | US23 | Μέιν | Maine | missing | 5 | missing | missing | メイン州 | 1 | missing | 3561 | missing | missing | 1 | 2 | missing | missing | 缅因州 | 0 | US-ME | missing | Maine | Maine | Maine | missing | Maine, US, United States | missing | مینے | missing | 2D Polygon | 3.5 | missing | missing | Maine | missing | US | missing | Maine | missing | 0 | Maine | missing | Мэн | missing | missing | USA | missing | missing | missing | Мен | 1 | State | 4971068 | 1 | 1159308501 | मेन | missing |
| 50 | missing | missing | missing | http://en.wikipedia.org/wiki/Michigan | Michigan | missing | United States of America | missing | USA | Michigan | 미시간 | Michigan | United States of America | US.MI | Michigan | missing | Michigan | missing | MI|Mich. | State | Q1166 | 1 | Michigan | missing | -1 | missing | -84.9479 | 1 | missing | Midwest | Michigan | -1 | East North Central | 2 | ميشيغان | 7.5 | 密歇根州 | میشیگان | missing | MI | 43.4343 | 20 | Michigan | missing | missing | missing | Michigan | -99 | US.MI | US26 | 2347581 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3562 | মিশিগান | מישיגן | Michigan | US26 | Μίσιγκαν | Michigan | missing | 8 | missing | missing | ミシガン州 | 1 | missing | 3562 | missing | missing | 1 | 2 | missing | missing | 密歇根州 | 0 | US-MI | missing | Mich. | Michigan | Michigan | missing | Michigan, US, United States | missing | مشی گن | missing | 2D Polygon | 3.5 | missing | missing | Michigan | missing | US | missing | Míchigan | missing | 0 | Michigan | missing | Мичиган | missing | missing | USA | missing | missing | missing | Мічиган | 1 | State | 5001836 | 1 | 1159314665 | मिशिगन | missing |
| 51 | missing | missing | missing | http://en.wikipedia.org/wiki/Alaska | Alaska | missing | United States of America | missing | USA | Alaska | 알래스카 | Alaska | United States of America | US.AK | Alaska | missing | Alaska | missing | AK|Alaska | State | Q797 | 6 | Alasca | missing | -1 | missing | -151.604 | 1 | missing | West | Alaska | -1 | Pacific | 2 | ألاسكا | 7.5 | 阿拉斯加州 | آلاسکا | missing | AK | 65.3609 | 20 | Alaska | missing | missing | missing | Alaszka | -99 | US.AK | US02 | 2347560 | missing | missing | 0 | US1 | missing | missing | missing | Admin-1 scale rank | 2 | missing | USA-3563 | আলাস্কা | אלסקה | Alaska | US02 | Αλάσκα | Alaska | missing | 6 | missing | missing | アラスカ州 | 1 | missing | 3563 | missing | missing | 1 | 2 | missing | missing | 阿拉斯加州 | 0 | US-AK | missing | Alaska | Alaska | Alaska | missing | Alaska, US, United States | missing | الاسکا | missing | 2D MultiPolygon | 3.5 | missing | missing | Alaska | missing | US | missing | Alaska | missing | 0 | Alaska | missing | Аляска | missing | missing | USA | missing | missing | missing | Аляска | 1 | State | 5879092 | 1 | 1159308731 | अलास्का | missing |
Get rid of Alaska, Hawaii and Puerto Rico. so we just have the continental US.
filter!(:name_en => ∉(("Alaska", "Hawaii", "Puerto Rico")), admin_1_df)
admin_1_df.geometry = GeoMakie.to_multipoly.(admin_1_df.geometry)
n = size(admin_1_df, 1)49In this case, the graph is a linkage from city to city, so we'll use the lat/long of each city as the position.
gpos = Dict(
(-96.5967, 38.9617) => "KSCYng",
(-122.3, 47.6) => "STTLng",
(-105.0, 40.75) => "DNVRng",
(-122.026, 37.3858) => "SNVAng",
(-87.6167, 41.8333) => "CHINng",
(-85.5, 34.5) => "ATLAng",
(-77.0268, 38.8973) => "WASHng",
(-73.9667, 40.7833) => "NYCMng",
(-86.1595, 39.7806) => "IPLSng",
(-95.5174, 29.77) => "HSTNng",
(-118.25, 34.05) => "LOSAng",
(-84.3833, 33.75) => "ATLAM5"
)Dict{Tuple{Float64, Float64}, String} with 12 entries:
(-122.026, 37.3858) => "SNVAng"
(-73.9667, 40.7833) => "NYCMng"
(-95.5174, 29.77) => "HSTNng"
(-96.5967, 38.9617) => "KSCYng"
(-122.3, 47.6) => "STTLng"
(-105.0, 40.75) => "DNVRng"
(-87.6167, 41.8333) => "CHINng"
(-77.0268, 38.8973) => "WASHng"
(-85.5, 34.5) => "ATLAng"
(-86.1595, 39.7806) => "IPLSng"
(-118.25, 34.05) => "LOSAng"
(-84.3833, 33.75) => "ATLAM5"From this Dict, we create a "complete", fully-connected graph. This means that each vertex is connected to each other vertex.
g = complete_graph(length(keys(gpos))){12, 66} undirected simple Int64 graphThe positions here are just the lat/long of each city, in the order they were added to the graph.
positions = Point2f.(collect(keys(gpos)))12-element Vector{Point{2, Float32}}:
[-122.026, 37.3858]
[-73.9667, 40.7833]
[-95.5174, 29.77]
[-96.5967, 38.9617]
[-122.3, 47.6]
[-105.0, 40.75]
[-87.6167, 41.8333]
[-77.0268, 38.8973]
[-85.5, 34.5]
[-86.1595, 39.7806]
[-118.25, 34.05]
[-84.3833, 33.75]Now, we create the figure and GeoAxis, in the lcc projection.
fig = Figure(size = (1200, 800), fontsize = 22)
ga = GeoAxis(
fig[1, 1],
source = "+proj=longlat +datum=WGS84",
dest = "+proj=lcc +lon_0=-100 +lat_1=33 +lat_2=45",
title = "Projection: lcc +lon_0=-100 +lat_1=33 +lat_2=45",
)GeoAxis with 2 plots:
┣━ Lines{Tuple{Vector{Point{2, Float64}}}}
┗━ Lines{Tuple{Vector{Point{2, Float64}}}}We plot the USA states as a sort of background material,
poly!(
ga, admin_1_df.geometry;
color = 1:n, colormap = (:viridis, 0.25),
strokecolor = :black, strokewidth = 1
)
fig
and finally execute the graph plot!
graphplot!(
ga, g;
layout = _ -> positions, node_size = 1,
edge_color = cgrad(:plasma)[LinRange(0, 1, 66)],
node_color = cgrad(:plasma)[LinRange(0, 1, length(keys(gpos)))]
)
fig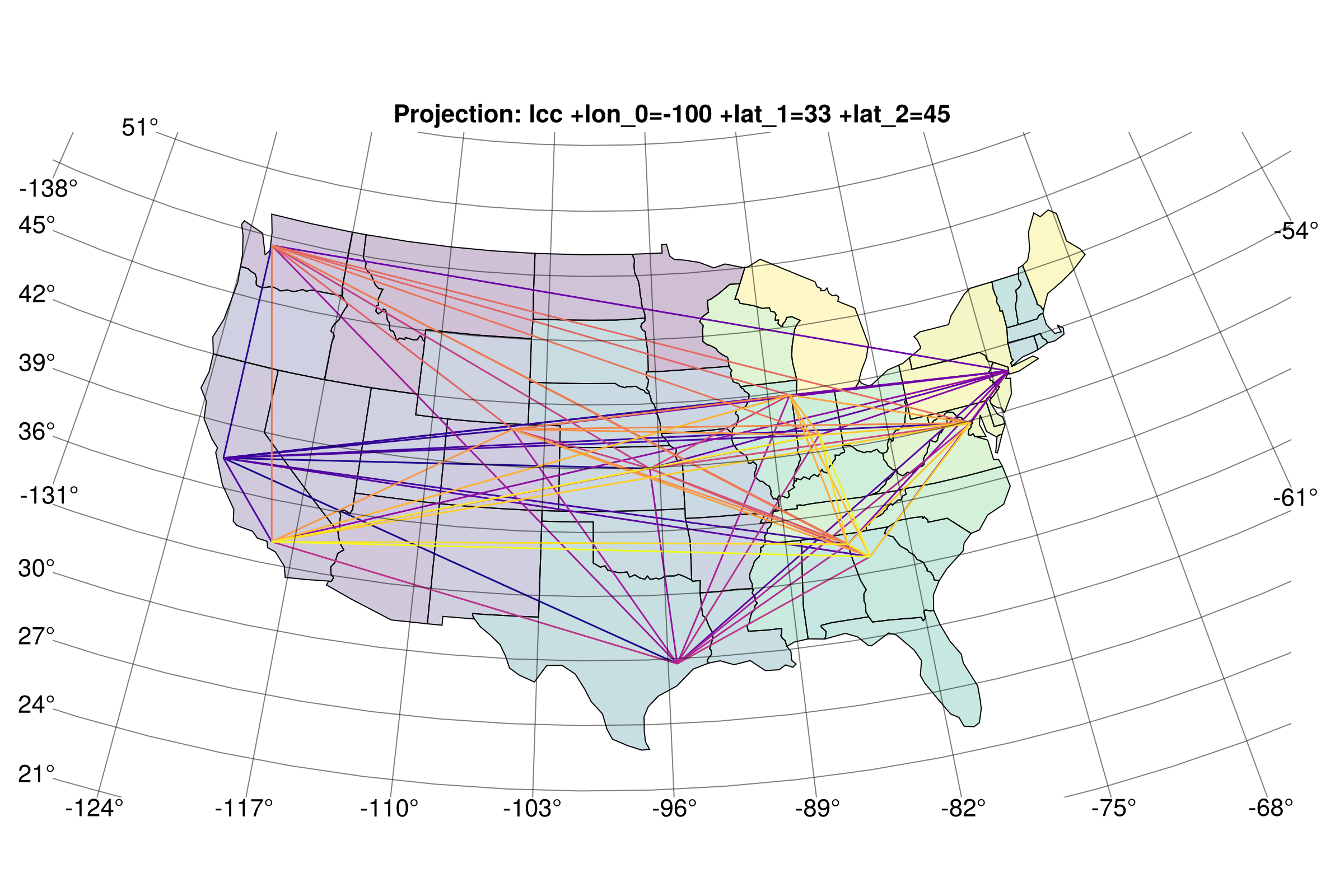
This page was generated using Literate.jl.